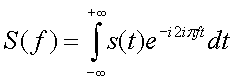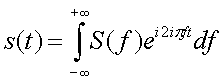Chapitre II. Qu’est ce qu’un son musical ?
Dans ce chapitre, on va essayer de visualiser certains sons à l’aide d’un oscilloscope électronique. Cette visualisation permettra de comprendre le passage de la notion de son à la notion de phénomène vibratoire qui sera la base des développements suivants.
Chapitre
II. Qu’est ce qu’un son musical ?
II.1.2. La
perception des sons
II.2. LE DISPOSITIF EXPERIMENTAL
II.3. Visualisation de differents sons
II.4. Avec des moyens modernes
II.6. Annexe 1 : Les figures, les conditions
expérimentales et l’exploitation des résultats
II.7. Annexe 2 : Transformée de Fourier
II.7.2. Intérêt
de la transformée de Fourier




II.1.
INTRODUCTION
II.1.1.
Généralités
Les sons perçus par l’oreille humaine sont en fait des variations de pression de l’air ambiant perçues par le tympan et transmis via l’oreille interne et le nerf auditif au cerveau qui va décoder les variations de pression « mesurées » et les transformer en « sons ».
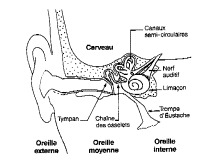
Figure II‑1 : Le sens de l’ouïe
|
|
|
|
|
|
|
|
Plus précisément, les variations de pression sont d’abord détectées « mécaniquement » par la membrane du tympan; ces « vibrations » sont ensuite transmises par la chaîne des osselets (voir Figure II‑2) au « limaçon » (ou cochlée); c’est dans le limaçon (voir Figure II‑3) que ces variations de pressions vont exciter de manière différentielle deux surfaces munies de cils (voir Figure II‑4); ce sont les mouvements différentiels de ces cils qui produiront des variations du champ électrique qui pourront alors être transmises au cerveau par l’intermédiaire du nerf auditif.
II.1.2.
La perception des sons
Chez l’homme, comme chez tous les vertébrés, l’organe permettant d’entendre est constitué par l’oreille. On distingue dans celle-ci trois parties distinctes qui sont l’oreille externe, l’oreille moyenne et l’oreille interne. L’oreille externe n’a pratiquement pas de rôle chez l’homme tandis que chez l’animal sa mobilité permet de localiser plus facilement les sons. Le conduit entre l’oreille externe et l’oreille moyenne est limité par le tympan qui est une fine membrane de 100 microns d’épaisseur. C’est le tympan qui le premier dans la chaîne de perception est mis en mouvement par les vibrations sonores (en fait des vibrations de la pression de l’air à l’extérieur qui peuvent être perçues car déphasées par rapport à la pression régnant dans un volume tampon formé par une cavité remplie d’air en relation, par la trompe d’eustache avec le larynx. (voir Figure II‑1).
|
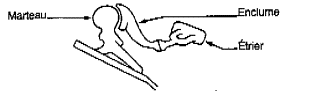
Dans cette cavité (oreille moyenne), une chaîne d’osselet, le marteau (malleus), l’enclume (incus) et l’étrier (stapes), est mise en vibration par le tympan (voir Figure II‑2). |
|
|
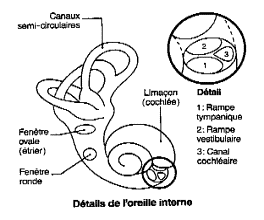
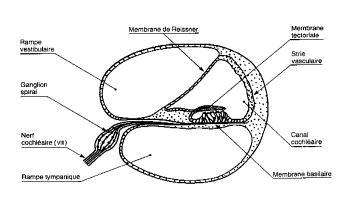
Ces osselets sont placés de telle façon qu’ils amplifient les vibrations transmises par le tympan, et les communiquent à l’oreille interne par l’intermédiaire de la fenêtre ovale (voir Figure II‑3). L’oreille interne est principalement constitué par la cochlée (ou limaçon) qui constitue le récepteur auditif à proprement parler (voir Figure II‑3et Figure II‑4). La cochlée est constituée d’un ensemble de trois canaux ou rampes dont deux contiennent un liquide proche du plasma, alors que le troisième, le canal cochléaire, contient un liquide de composition très différente qualifié d’endolymphe. |
|
|
L’organe sensoriel qui va convertir les vibrations transmises par les différents canaux en signaux (électrique) perceptibles par le système nerveux central est l’organe de Corti et est situé à la limite entre le canal cochléaires et la rampe tympanique. Cet organe contient des cellules ciliées disposées en rangées. L’ensemble de ces cellules est recouvert d’une membrane gélatineuse, la membrane tectoriale dans laquelle viennent se fixer les cils des cellules ciliées. |
|
|
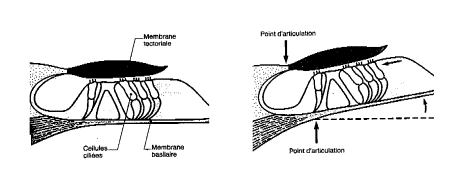
Les vibrations sonores sont ainsi transmises par la chaîne des osselets sur la fenêtre ovale, puis au travers des différentes rampes jusqu’au niveau de la fenêtre ronde. Les liquides étant incompressibles, la membrane limitante de celle-ci vibre au même rythme que l’étrier qui ferme la fenêtre ovale. Les mouvements du liquide de la rampe vestibulaire provoquent la déformation des membranes limitantes du canal cochléaire et plus particulièrement de la membrane basilaire (voir Figure II‑5). La membrane tectoriale qui recouvre les cellules sensorielles étant fixée dans la région médiane de la cochlée, le mouvement relatif de ces deux membranes provoque alors un fléchissement rythmique des cils des cellules réceptrices. Ainsi, les vibrations perçues par le tympan sont transformées en mouvements des cils des cellules sensorielles. Ce sont ces mouvements qui seront codées en un message sensoriel transmis par le nerf cochléaire. |
|
|
La transformation des mouvements des cils en signaux électriques est faite dans l’organe de Corti; la descriptions précise des phénomènes mis en jeu dépasse le cadre de cet ouvrage, mais on pourra consulter utilement la référence [14], d’ou sont tirés les renseignements de ce paragraphe, pour plus d’information sur le sujet.
De la même manière, un haut parleur (ou un micro) est capable de transformer des variations de pressions en variations de courant (fonction micro) et vice-versa (fonction haut-parleur).
Il est donc possible, si on veut visualiser
les variations de pressions qui correspondent à un son donné, de transformer
par le biais d’un système analogue au haut-parleur ces variations de pressions
en variations de courants. C’est l’approche que l’on va suivre dans ce chapitre
pour examiner différents sons et/ou bruits.
II.2.
LE DISPOSITIF
EXPERIMENTAL
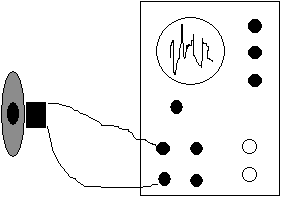
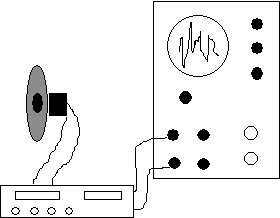
Pour mesurer les variations de pressions correspondant à un son donné, nous allons nous servir d’un oscilloscope électronique qui sera attaqué par la sortie d’un haut-parleur, amplifiée ou non. On pourra dans certains cas attaquer cet oscilloscope directement par la sortie analogique d’un appareil « producteur de sons » tels qu’un orgue ou un piano électronique.
Le dispositif est le suivant :
|
|
|
Figure II‑7 : Branchement avec amplification
|
II.3.
Visualisation de
differents sons
II.3.1.
La voie humaine
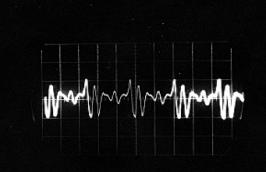
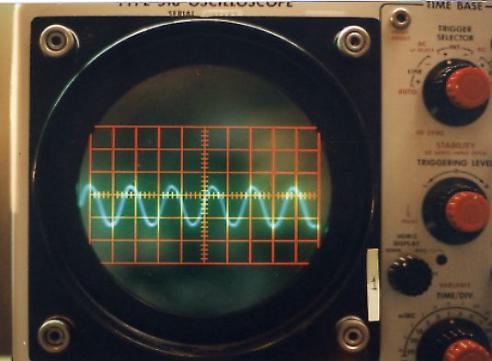
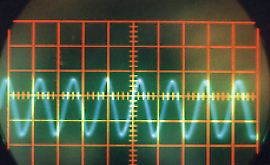
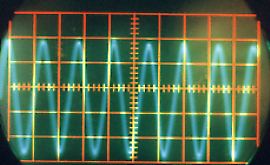
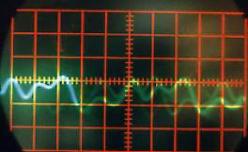
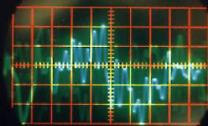
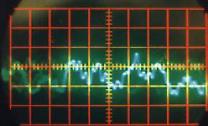
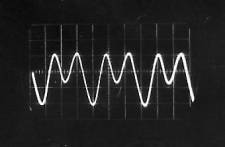
La photographie de la Figure II‑6qui présente le dispositif expérimental a été prise alors qu’une chanson était chantée. On constate sur l’écran une superposition de différentes courbes oscillant autour de l’axe horizontal. Cette superposition de différentes courbes qui forment un nuage, provient du fait que le signal reçu par l’intermédiaire du micro-haut-parleur n’est pas stable en fréquence. L’impression de plusieurs courbes est du à la rémanence à la fois de l’écran et de l’œil. Pour obtenir un signal plus stable, nous avons repris l’expérience avec différents sons « simples ».
Différents sons ont été visualisés et les résultats sont présentés sur les figures 2-7 à 2-15 ci-après:
|
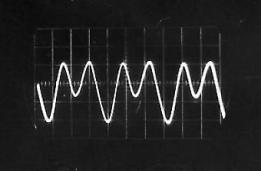
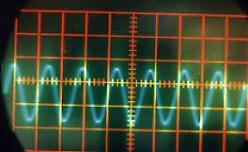
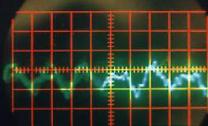
Figure II‑8 |
Son correspondant à la voyelle « A » |
|
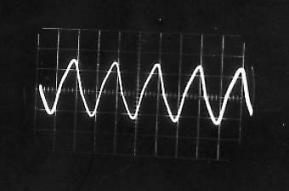
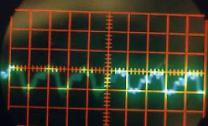
Figure II‑9 |
Son correspondant à « LA » |
|
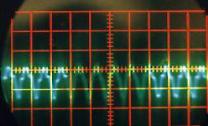
Figure II‑10 |
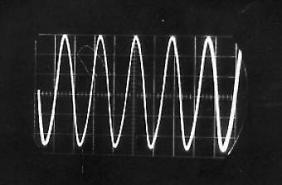
Son correspondant à la voyelle « I » |
|
Figure II‑11 |
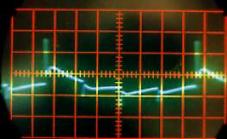
Son correspondant à la voyelle « O » (faible) |
|
Figure II‑12 |
Son correspondant à la voyelle « O » (fort) |
|
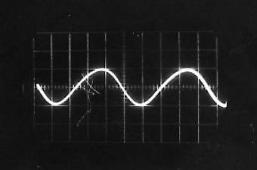
Figure II‑13 |
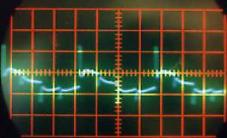
Son correspondant à « OU » |
|
Figure II‑14 |
Son correspondant à la voyelle « U » (faible) |
|
Figure II‑15 |
Son correspondant à la voyelle « U » (fort) |
|
Figure II‑16 |
Son correspondant à la voyelle « E » |
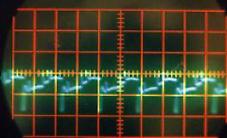
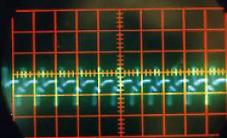
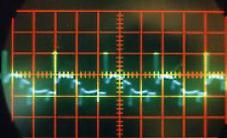
Pour chacun de ces sons, et au contraire de la chanson, on obtient des signaux stables clairement visibles sur l’écran de l’oscilloscope.
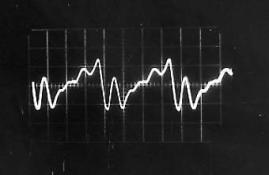
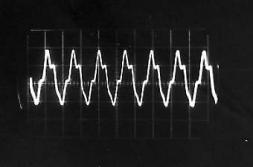
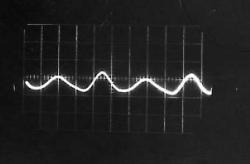
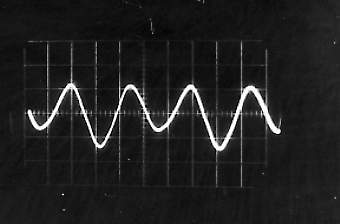
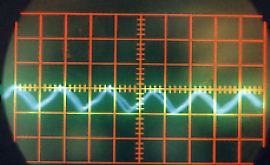
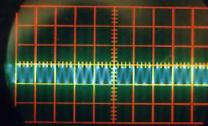
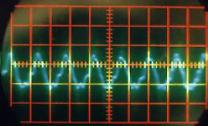
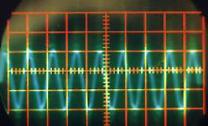
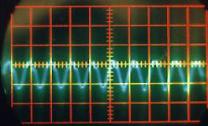
Quel que soit le son émis, on constate qu’il correspond à une variation périodique de la pression de l’air. Cette fonction périodique peut varier de la fonction la plus simple qui ressemble à une sinusoïde comme par exemple le « OU » sur la Figure II‑13, à des fonctions plus complexes comme celle qui correspond au « A » sur la Figure II‑8.
Une analyse par transformée de Fourier de chacun de ces sons pourrait nous indiquer quelles sont les fonctions « sinusoïdales » qui constituent chacun de ces sons; on pourrait ainsi en déduire d’abord la fonction correspondant à la période de la fonction, et les autres fonctions de périodes plus petites qui permettent de reproduire les fonctions représentées (on verra plus tard que la première est le fondamental d’un son, les autres, les harmoniques). D’ailleurs, sur la Figure II‑8, on distingue parfaitement au delà de la période principale (qui mesure 1,4 cm sur la photographie), la présence d’autres fonctions de périodes de 0,7 cm et 0,35 cm, c’est à dire de périodes égales à la moitié et au quart de la période principale. On pourra vérifier le même phénomène sur les autres sons « plus complexes » comme ceux des Figure II‑9, Figure II‑10et Figure II‑12.
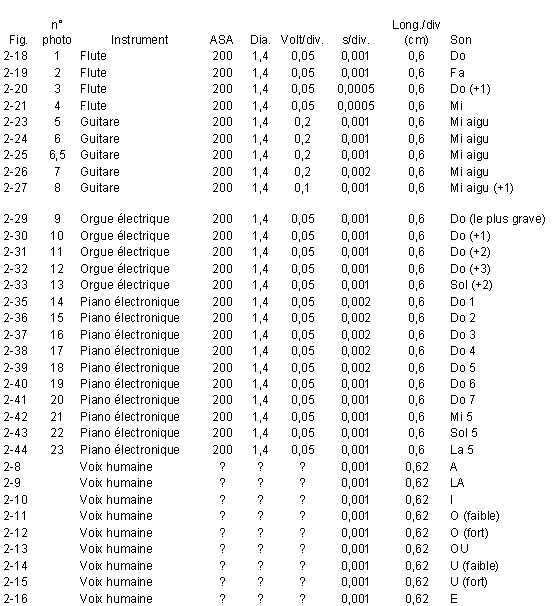
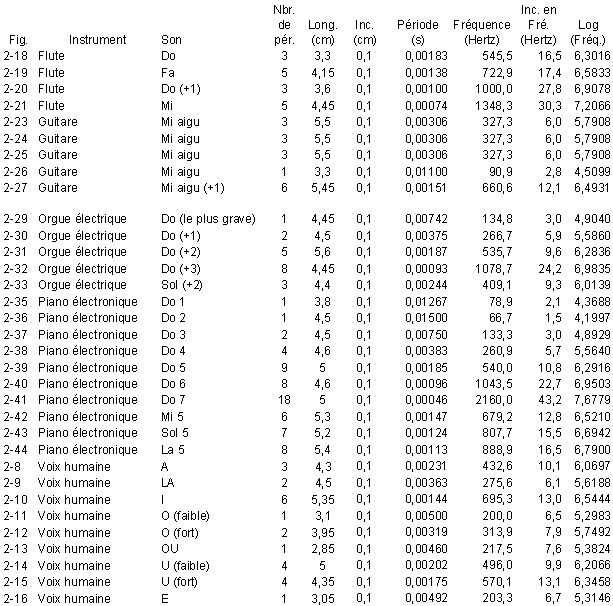
Les photographies représentées sur ces figures ayant été prises sans que l’on note les réglages de l’oscilloscope, et plus particulièrement, sans que l’on note la période du balayage horizontal, il n’est pas possible de mesurer, à posteriori, la fréquence de ces sons. Néanmoins, par analogie et compte tenu des essais réalisés pour les paragraphes suivants, on a tenté de retrouver les réglages possibles (voir annexe); on trouve alors des fréquences allant de 200 Hertz pour le « O » à 700 Hertz pour le « I », ce qui correspond aux possibilités du baryton (voir chapitre 1, figure 1-17).
|
|
|
|
Figure II‑9 : Le son «syllabe LA » |
|
|
|
|
Figure II‑11 : Le
son « voyelle O faible » |
|
|
|
|
Figure II‑13 : Le son
« syllabe OU » |
|
|
|
|
Figure II‑15 : Le son voyelle U fort » |
II.3.2.
La flûte
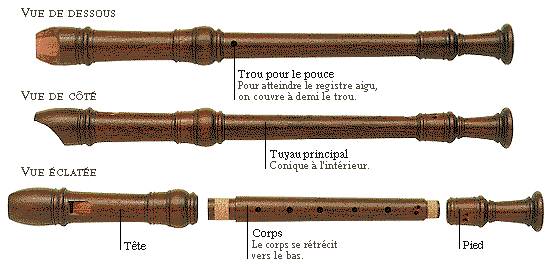
La même expérience a été reprise avec une flûte d’écolier (voir figure 2-17 ci-dessous), pour laquelle nous avons chercher à visualiser le « premier » Do et le Fa de la même octave (figures Figure II‑18et Figure II‑19), ainsi que le Do et le Mi de l’octave supérieure (Figure II‑20et Figure II‑20).
On constate tout d’abord que les sons émis sont très pur; on ne distingue pratiquement pas d’harmoniques au contraire de ce que l’on avait observé pour la voie humaine.
Les fréquences mesurées sont les suivantes (voir pour les détails l’annexe) :
Do : 546 ± 17 Hertz, ce qui correspond à peu prés au Do4 (ou Do #4) - voir chapitre 3, tableau 2-1 -
Fa : 723 ± 17 Hertz, ce qui correspond au Fa4
Do (+1) : 1000 ± 30 Hertz, ce qui correspond en tenant compte des incertitudes, au Do5
Mi : 1350 ± 30 Hertz, ce qui correspond au Mi5.
On constate que le Do (+1) a une fréquence proche du double de celle du Do.
Figure II‑17 :
Flûte
d’écolier
|
Figure II‑18 : Flûte : Do |
|
|
|
|
|
|
|
Figure II‑20 : Flûte : Do (+1) |
|
|
II.3.3.
La guitare
La même expérience a été reprise avec une guitare. Pour la guitare, et du fait des difficultés pratique de réalisation (haut-parleur-micro posé sur la caisse de résonance, amplitude du son variant rapidement,...), nous n’avons considéré que la note Mi, mais sur deux octaves différentes.
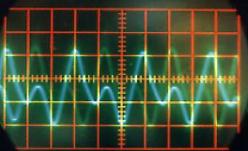
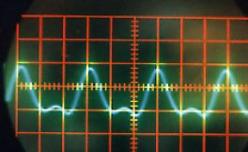
Nous avons pris quatre clichés du Mi de la première octave mais joué avec des « touchés » différents; on constate que si la fréquence du fondamental est remarquablement stable et égale à 330 hertz (ce qui correspond au Mi3 - voir Chapitre 3 tableau 1-2), la forme de la courbe varie fortement d’un cliché à l’autre.
Les harmoniques qui se superposent au fondamental, et qui sont décelables, ont clairement des périodes égales à la moitié et au quart de la période du fondamental. Il faut noter que ce Mi a été joué avec la corde mince.
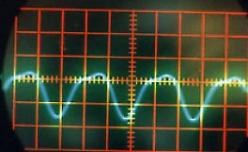
Par contre le Mi de l’octave supérieure, dont la fréquence à 660 Hertz est exactement la double de la précédente, a très peu d’harmoniques. Ce Mi a été joué en pinçant la corde mince au milieu.
|
|
|
|
|
|
|
|
|
|
|
|
|
II.3.4.
Un orgue électrique
La même expérience a été reprise avec un orgue électrique.
Nous quittons ici la réalité du son musical, pour aborder les caractéristiques des instruments électroniques qui ont pour but de simuler un instrument réel. L’orgue utilisé pour cette expérience date de la fin des années 1960, et représente donc un des premiers stades de la simulation électronique des instruments de musique (voir Figure II‑28).
Nous avons visualiser les quatre Do successifs (Figure II‑29à Error! Reference source not found.) ainsi que le Sol de la deuxième octave disponible.
Au niveau des fréquences on obtient pour les Do : 135, 267, 536 et 1078 qui correspondent effectivement au quatre Do successifs et dont le premier est le Do2. La fréquence de chacun de ces Do (à l’exception du premier) est bien double de celle du Do précédent.
Le Sol testé, avec une fréquence de 400 Hertz correspond au Sol3.
Par contre on constate que les sons ont été grossièrement reconstitués, seule la fréquence ayant réellement cherché à être retranscrites.
Figure II‑28 : Orgue électrique
|
|
|
|
|
|
|
|
|
|
|
|
|
|
II.3.5.
Le piano électronique
La même expérience a été reprise avec un piano électronique de type Yamaha « Clavinova » (Figure II‑34) dont la conception remonte à la fin des années 1980. On constate sur les figures 2-30 à 2-39 les progrès réalisés par rapport à l’orgue électronique du paragraphe précédent.
On a d’abord cherché à visualiser la gamme complète des Do (Figure II‑35à Figure II‑41). A partir du deuxième, on retrouve les fréquences des Do telles que calculées au chapitre 3, le Do2 de l’expérience correspondant au Do1. Par contre pour le premier Do, la fréquence est très difficile à lire; en fait on ne voit pas sur la photographie une période complète, mais seulement sans doute une demi-période par défaut du réglage. La fréquence calculée pour ce Do doit correspondre à la demi-période ce qui est cohérent avec la valeur trouvée pour le Do suivant.
On retrouve aussi pour les Mi, Sol et La testés (Figure II‑42 à Figure II‑44), les fréquences des notes correspondantes selon le tableau 1-2 du chapitre 3.
On constate pour chaque note la présence d’harmoniques, mais d’autant moins que la fréquence est plus élevée; on en comprendra la raison dans les chapitres suivants.
Figure II‑34 : Piano électronique

|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
II.4.
Avec des moyens modernes
Les premières photographies, en noir et blanc, des signaux correspondant à la voie humaine, ont été prises au milieu des années 70. Depuis, la technologie a évolué, et on peut maintenant en quelques minutes, enregistrer un son, le stocker sur ordinateur, et en calculer le spectre fréquentiel par un outil basé sur des transformées de Fourier. C’est ce que nous avons fait ici, sur un piano et sur toutes les notes DO d’un piano droit.
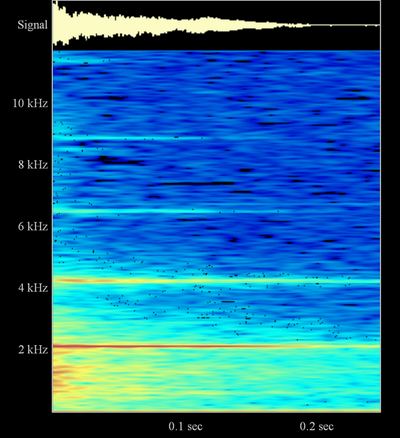
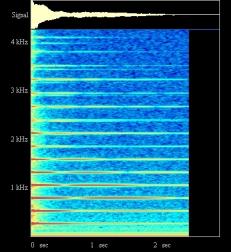
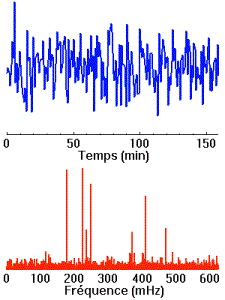
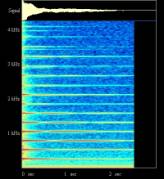
Les représentations ci-dessous montrent dans la partie haute, l’amplitude du signal – on constatera un son qui monte très vite quand on actionne la touche, et qui s’atténue ensuite assez rapidement. Dans la partie basse (la plus colorée), c’est, en fonction du temps, l’intensité du son (mesurée en db), représentée par une échelle de couleur, en fonction de la fréquence (axe des Y).
|
|
Figure II‑45 :Piano droit -
DO 1 Sur ce premier essai, le DO le plus aigu du piano, on distingue de l’ordre de 5 fréquences pour lesquelles l’intensité est nettement plus forte que pour le reste de la gamme de fréquences. Pour ces cinq fréquences, la plus basse, mesurée de l’ordre de 2130 Hertz, est celle qui tient le plus longtemps et la plus intense ; les autres sont d’autant plus fugitives que plus hautes, et d’autant moins intense. Ces fréquences sont séparées les unes des autres par la fréquences de la première (à la précision de mesure près) ; elles sont appelées les harmoniques. La fréquence la plus forte, caractéristique de la note est le fondamental. Les fréquences
mesurées sont : 2130 4286 6519 8906 |
|
|
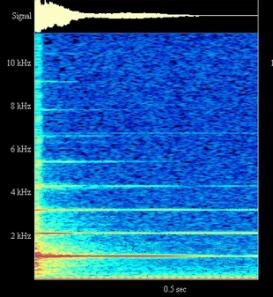
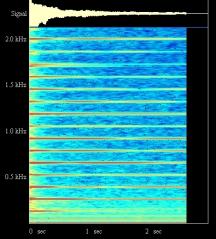
Figure II‑46 :Piano droit -
DO 2 On retrouve sur le deuxième DO du clavier, les mêmes phénomènes que ceux identifiés sur le premier en ce qui concerne le fondamental et les harmoniques. Les harmoniques sont séparées entre elles par la fréquence du fondamental, 1075 Hertz, moitié de celle du premier DO. Les fréquences
mesurées sont : 1075, 2150, 3224, 4315, 5437, 6607 Hertz. |
|
|
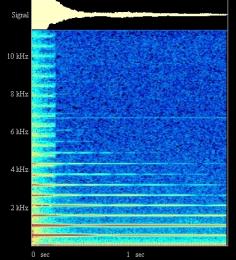
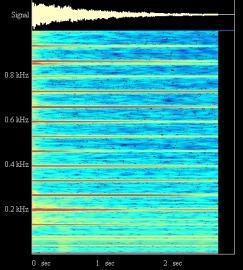
Figure II‑47 :Piano droit -
DO 3 Toujours les mêmes constatations. On note aussi que les fréquences les plus graves sont celles dont le son dure le plus longtemps. Le fondamental est ici un peu plus faible que la moitié du fondamental du do précédent ; le piano pourrait être mieux accordé… Les fréquences mesurées sont: 533, 1065, 1586, 2118, 2663, 3207, 3763 Hertz |
|
|
|
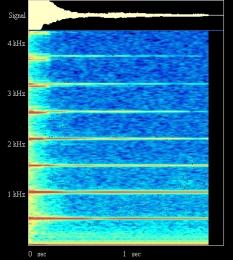
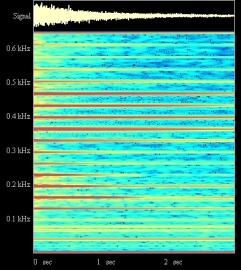
Figure II‑48 :Piano droit -
DO 4 Ñ Fréquences du fondamental: 268 Hertz Figure II‑49 :Piano droit -
DO 5 Ò Fréquences du fondamental: 130 Hertz |
|
|
|
Figure II‑50 :Piano droit -
DO 6 Ñ Fondamental:
67 Hertz Figure II‑51 :Piano droit - DO 7 Ò Fondamental:
38 Hertz |
|
Cette analyse a permis de dégager les constatations suivantes, lors du jeu d’une note de piano :
- Le son obtenu est composé de la superposition de plusieurs sons de fréquences toutes multiples de la fréquence la plus basse ; on appellera celle-ci la « fondamentale », les autre, les harmoniques.
- L’intensité de la fréquence la plus basse des sons, est nettement plus importante que celles de ses harmoniques.
- Il y a d’autant plus d’harmoniques que le fondamental est plus grave
- Les sons correspondants aux fréquences les plus basses sont ceux qui perdurent le plus longtemps.
D’une manière, certes, plus précise, cette analyse permet de confirmer ce que nous avions pu visualiser avec les expériences utilisant un oscilloscope.
II.5.
CONCLUSION
Grâce aux possibilités de visualisation de l’oscilloscope électronique utilisé, nous avons pu tirer déjà quelques observations sur la réalité du son musical que l’on peut résumer de la façon suivante:
- Un son musical «(stable ) correspond à un signal oscillatoire stable
- Un son musical est caractérisé par une fréquence fondamentale, et des harmoniques de fréquences multiples du fondamental, mais dont l’amplitude dépend de la façon de jouer la note, mais surtout de l’instrument.
- La superposition dénombrable de sons musicaux (au cours d’une chanson par exemple), bien que conduisant à des signaux plus compliqués, est toujours « musicale »
- Les sons musicaux courants ont des fréquences pouvant aller de quelques dizaine de Hertz à quelques milliers d’Hertz.
II.6.
Annexe 1 : Les
figures, les conditions expérimentales et l’exploitation des résultats