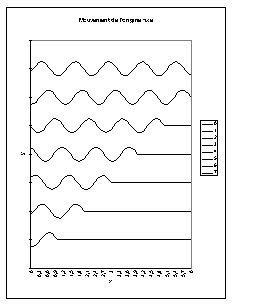
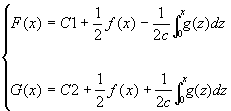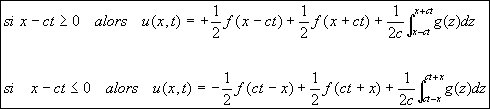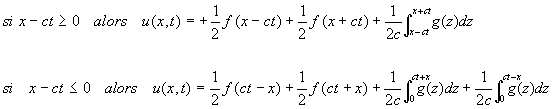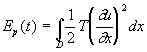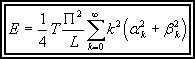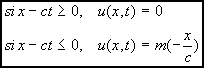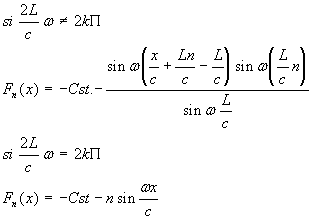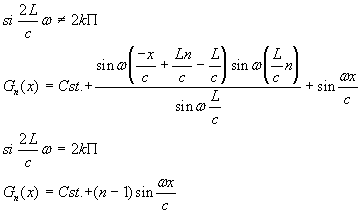Chapitre IV. Analyse d’une corde vibrante
Nous allons dans ce chapitre analyser de quelle façon une corde tendue peut être mise en vibration suite à une excitation initiale, et comment le mode de vibration peut dépendre des caractéristiques de cette excitation.
Chapitre
IV. Analyse d’une corde vibrante
IV.2. resolution de l’equation - Solution générale
IV.3. Solutions particulières - Etat de la corde
définie à t=0
IV.3.2. Corde fixée à une extrémité
IV.3.3. Corde fixée aux deux extrémités
IV.3.4. Corde dont une des extrémité est libre
IV.4. Propriétés des solutions de l’equation des
ondes
IV.4.1. Décomposition en fonctions périodiques pour une corde de
longueur L
IV.5. cas ou la corde est soumise à une force
extérieure
IV.5.2. Corde ayant une extrémité dont le déplacement est imposé.
IV.6.1. Annexe 1 : Corde infinie
IV.6.2. Annexe 2 : Positions pour une corde fixée à une
seule extrémité
IV.6.3. Annexe 3 : Positions pour une corde fixée aux deux
extrémités
IV.6.4. Annexe 4 : Vitesses pour une corde fixée à une
extrémité
IV.6.5. Annexe 5 : Vitesses pour corde fixée aux deux
extrémités
IV.6.6. Annexe 6 : Corde infinie – Dirac en vitesse
IV.6.7. Annexe 7 : Positions pour une corde fixée aux deux
extrémités – dirac en vitesse à 0
IV.6.8. Annexe 8 : Simulation d’une corde fixée à une seule
extrémité par une corde infinie
IV.6.9. Annexe 9 : Positions pour une corde fixée à une
seule extrémité
|
|
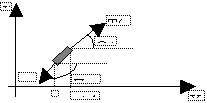
IV.1. Mise en équation
Nous allons considérer une corde de longueur « L » tendue entre deux points, et dont la tension est « T » exprimée en Newton. La masse linéaire de la corde sera appellée « r ».
Nous allons écrire l’équation du mouvement d’une portion « dx » de la corde; nous considérerons que cette corde n’est pas élastique et que les mouvements sont « petits ».
Figure IV‑1 Schématisation
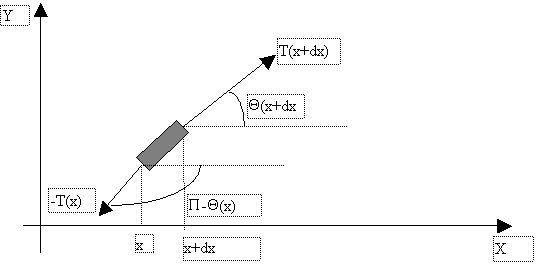
Si les mouvements sont petits,Q est petit et la longueur de l’élément de corde est aussi dx (dx/cosQ); on a alors :
Or si la corde est non élastique, T est constant en fonction de x et sera nommé simplement T, on a alors:
i
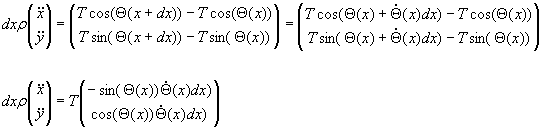
D’ou en ne développant les fonctions circulaires qu’au premier degré:
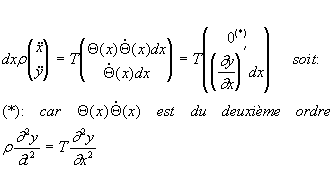
soit en écrivant 
on a:
|
|
(1)
qui est l’équation des ondes unidimensionnelles.
IV.2. resolution de
l’equation - Solution générale
Pour résoudre l’équation (1), on va procéder au changement de variable suivant:
On va calculer les dérivées secondes de y en x et t, en fonction de celles en a et b. On peut écrire:
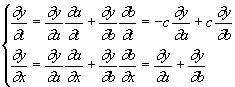
et ainsi
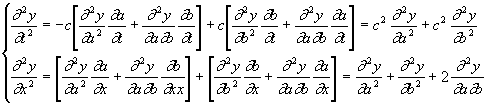
or ces deux expressions satisfont (1) et donc:
|
|
donc
y est donc la somme d’une fonction de a et d’une fonction de b, on peut alors écrire que la solution générale de (1) est :
|
|
(2)
De cette expression (2), on peut déduire une propriété caractéristique des solutions de l’équation 1. En effet si on considère x et x’ deux points de la corde tels que x’ est supérieur à x, on peut écrire:
ce qui signifie que la déformation en x’ à t’=t+(x’-x)/c est égale à la déformation qu’il y avait à x à l’instant t; cette déformation s’est donc propagée dans le sens positif à la vitesse c.
De même, on peut vérifier que G correspond à une déformation se déplaçant dans le sens des x négatifs à la vitesse c.
y est donc la somme de la propagation en directions opposées de deux déformations, constantes dans le temps et se propageant à la vitesse c.
IV.3. Solutions
particulières - Etat de la corde définie à t=0
IV.3.1. Corde infinie
IV.3.1.a.
Expression de la
solution
Considérons une corde infinie u(x,t), u étant l’ordonnée du point d’abscisse x à l’instant t, et dont l’état à l’instant 0 est définie par la fonction y=f(x) pour la position et g(x) pour la vitesse axiale .
On a alors:
|
|
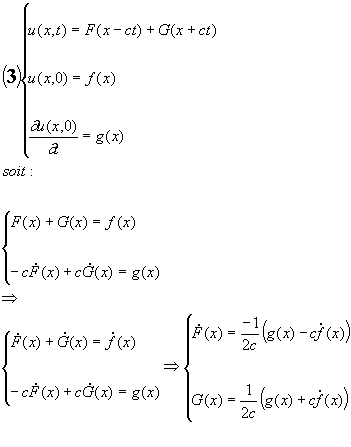
(4)
Or d’après (3), C2=-C1 et donc :
|
|
(5)
IV.3.1.b.
Exemple :
Vitesse initiale nulle
Examinons sur un exemple simple ce à quoi conduit cette expression.
On considérera que la vitesse initiale de la corde est nulle (g(x)=0), et on prendra pour f une fonction « triangle) de hauteur « 1 » et de base « 2 ». On considéra aussi que la vitesse c est égale à 1.
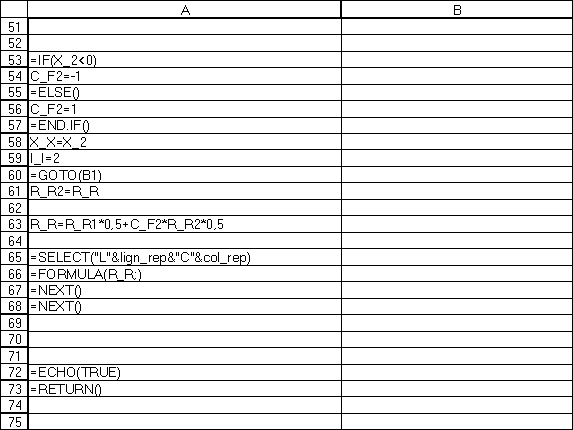
La simulation présentée sur la figure 4.2, ainsi que les autres simulations présentées dans le reste de ce chapitre, sont obtenues à l’aide du logiciel EXCELL; les programmes utilisés sont donnés pour informations dans les annexes (voir ici IV.7.1 page 36).
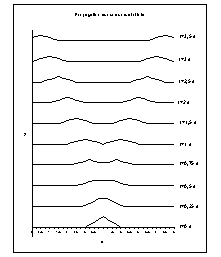
Figure IV‑2 : Propagation sur une corde infinie
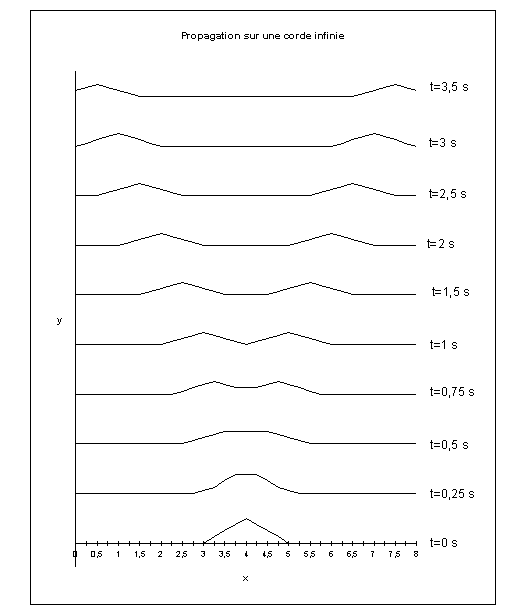
On constate de manière évidente, la présence des deux perturbations se dirigeant dans des directions opposées. Les conditions initiales, symétriques, entraînent que ces déformations sont, en absolue, « égales » (c’est à dire image l’une de l’autre par translation).
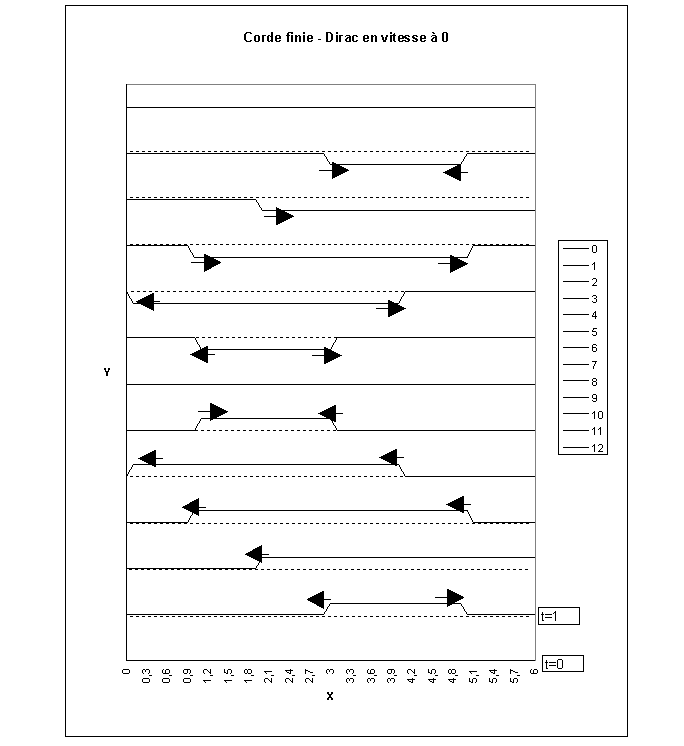
IV.3.1.c. Exemple : Vitesse initiale de la forme d’un Dirac
Dans ce paragraphe nous examinons une situation initiale « inverse » de la précédente; nous supposerons que la corde n’est pas déformée à l’instant 0, mais que l’on est capable d’imposer à un de ces points une vitesse non nulle. Nous définirons ainsi la fonction g par un Dirac d’intégrale égale à la vitesse voulue.
La simulation obtenue est présentée sur la figure suivante (voir IV.7.6 page 46).
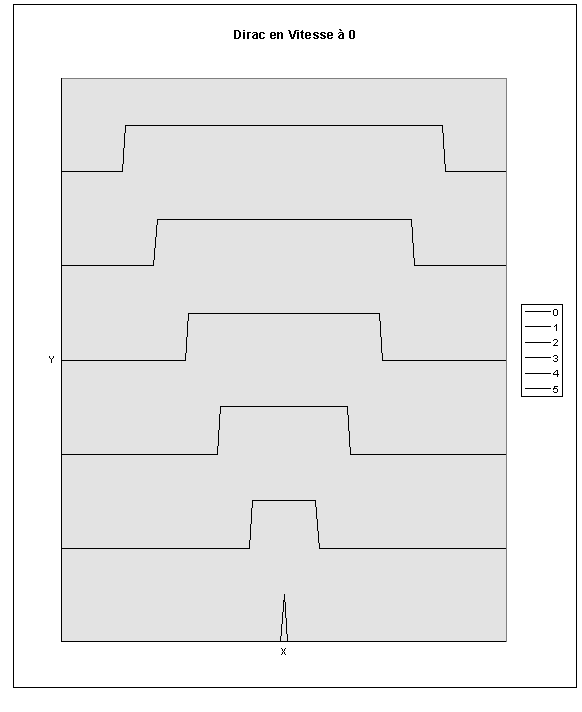
Figure IV‑3 :Dirac en vitesse en O
Comme précédemment, on retrouve la présence de deux déformations se propageant dans des directions opposées; la corde se déplace dans la direction de la vitesse initiale d’une quantité déterminé (égale à la vitesse imposée divisée par c).
IV.3.2. Corde fixée à une extrémité
IV.3.2.a.
Expression de la
solution
Considérons une corde fixé en 0, et définie pour x>0. L’équation (5) ne définie u(x,t) que si f et g sont définis.
Comme la corde correspond à x>0, f et g ne sont définis que pour des réels positifs. Il faut donc revenir au système (3) complétée de la condition u(0,t)=0 pour pouvoir définir F et G.
En fait, il faut et il suffit de définir F pour les valeur négatives de « x-ct ».
Pour cela, on utilise la relation
|
|
qui conduit à
|
|
soit : (6)
On en déduit immédiatement que :
|
|
(7)
L’équation (6) nous indique en fait, si on reprend l’interprétation obtenue au paragraphe précédent et concernant la propagation des déformations à la vitesse c, que lorsque la déformation se propageant vers les x négatifs atteint 0, elle se réfléchie et repart vers les x positifs en étant inverse de la fonction G.
En effet,
On vérifiera aisément que pour x-ct
0, alors G(ct-x) représente la déformation, inverse par
rapport à l’axe des x, de F, et se déplaçant dans le sens positif comme G.
Ce phénomène est clairement mis en évidence dans l’exemple suivant.
IV.3.2.b.
Exemple :
Vitesse initiale nulle
On reprend le cas présenté au $3.1.1, mais en fixant la corde en 0, et en ne considérant que les x positifs.
La figure 4.4 présente l’évolution de la déformation de la corde en fonction du temps (voir IV.7.2 page 38).
Figure IV‑4 : Corde fixée à une extrémité
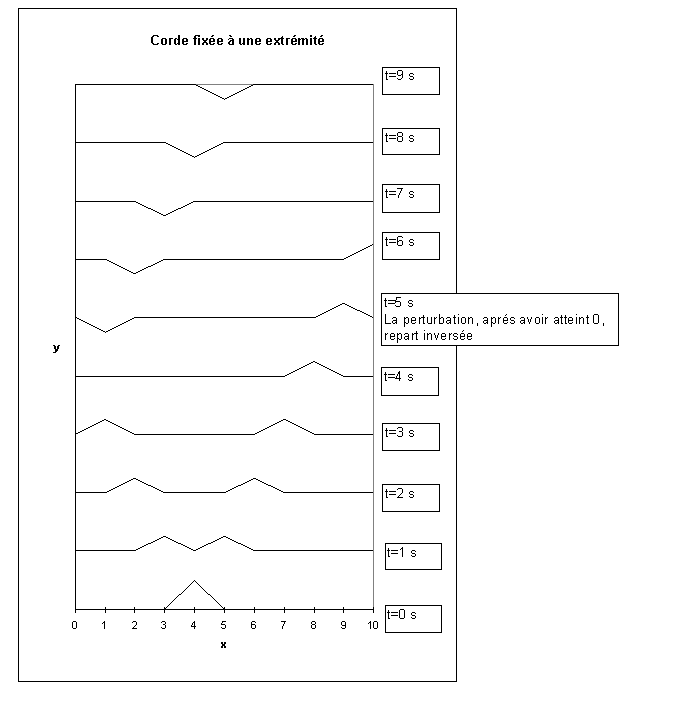
A t=3s, la partie « gauche » de la déformation se
déplaçant vers 0, atteint 0; à t=4 s, la déformation a disparue et se retrouve
après t=4s inversée par rapport à la déformation initiale et se déplaçant vers
la droite. La figure 4.5 ci-après présente un « zoom » effectué lors
de la réflexion en 0.
Figure IV‑5 : Réflexion de l’onde en zéro
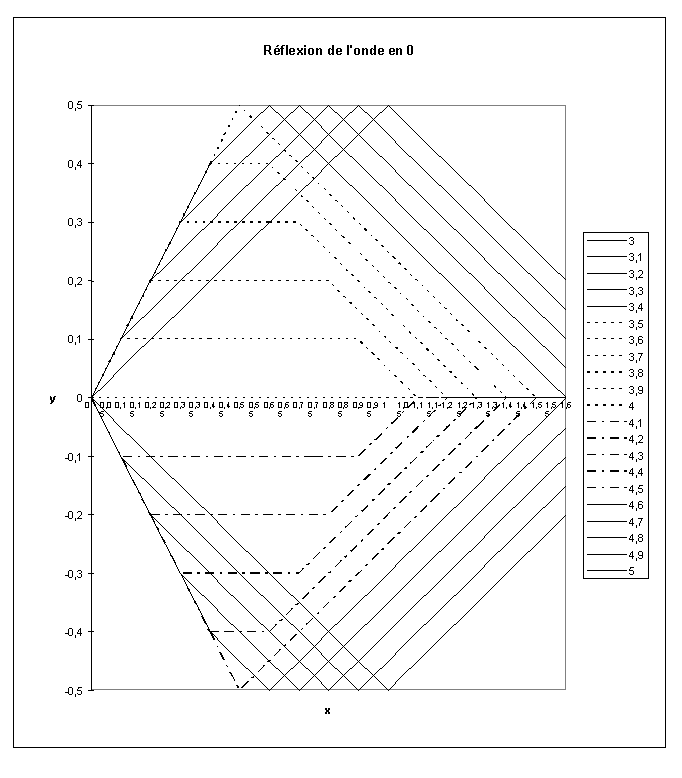
Une fois que l’extrémité gauche de la déformation atteint 0, la déformation « se tasse » et la longueur de sa base tend vers 1 quand t tend vers 4. Au delà de 4 la corde se déforme de manière symétrique par rapport à l’arrivée de la déformation. La vitesse de propagation de l’onde sur la corde est égale à la moitié de la vitesse « verticale ».
Les figures 4.6 et 4.7 indiquent les champs de vitesse correspondant aux figures 4.4 et 4.5.
On obtient évidemment lors de la propagation du « triangle », des vitesses constantes et opposées pour les x correspondant à chaque coté du triangle. A t= 4s, la vitesse de la partie en mouvement est double de la vitesse que l’on constate sur une zone « libre » de la corde. En fait, sur la partie de la corde sur laquelle se produit une « compression » de la déformation résultant en une réflexion, la vitesse est multipliée par deux tant que la déformation est présente (voir IV.7.4 page 42).
Figure IV‑6 : Corde fixée à une extrémité
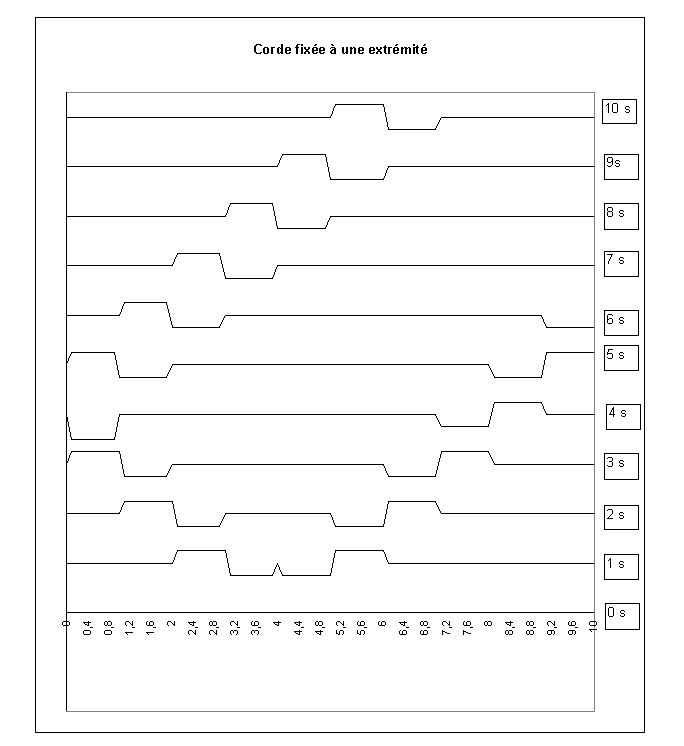
Figure IV‑7 : Vitesse lors de la réflexion en O
On peut interpréter ce phénomène de réflexion sur une extrémité fixe par analogie avec la propagation de plusieurs fronts d’onde sur une courbe infinie.
Si on reprend l’exemple qui précède en considérant cette fois une corde infinie, dont les conditions initiales pour les x positifs sont égales aux conditions initiales de la corde fixée en 0 considérée précédemment. Pour la partie de la corde correspondant aux x négatifs, on peut reproduire l’inverse de la déformation initiale de la corde « positive ». Par inverse, on entends symétrique par rapport au point 0.
Si on calcule alors la propagation des différents fronts d’ondes, on constatera que deux fronts d’onde opposées, se dirigent au début vers le point O; la première correspond à l’onde crée par la déformation de la partie positive de la corde qui se déplace vers les x négatifs; la deuxième étant l’onde crée par la déformation de la partie négative de la corde et qui se déplace vers les x positifs. Ces deux ondes étant inverses l’une de l’autre, leurs contributions au déplacement du point O s’annuleront à tous les instants.
Ce processus est illustrée sur la figure ci-dessous (voir IV.7.8 page 49).
IV.3.3. Corde fixée aux deux extrémités
IV.3.3.a.
Expression de la
solution
Comme précédemment, on va dans ce cas observer la superposition de deux ondes se déplaçant entre les deux extrémités de la corde et se réfléchissant sur ces même extrémités.
Pour calculer F et G, il faut écrire, si la corde est de longueur L, en plus des équations (3) :
u(0,t) =0
u(L,t)=0
f et g étant définies sur [0,L], il faut définit F et G sur R en utilisant les deux fonctions précédentes.
Sur [0,L], F et G sont définies par les équations (3);
Sur [L,2L], on écrit :
G(x)=G(L+ct)=-F(L-ct) (t=(x-L)/c)
F(x)=F(L+ct)=-G(L-ct) (t=(x-L)/c)
Sur [2L,3L], on applique la même méthode et on obtient:
G(x)=G(2L+ct)=-F(2L-ct)=-F(L+(L/c-t)c)=G(L-c(L/c-t)=G(ct)
et de même F(x)=F(2L+ct)=F(ct)
On applique la même méthode pour [nL,(n+1)L] avec n entier relatif pour construire F et G sur R.
On constate que F et G sont périodiques, et de période 2L.
On a donc aussi u(x,t)=F(x-ct)+G(x+ct)=F(x-ct-2L)+G(x+ct+2L)=u(x,t+2L/c)
|
u est périodique en temps de période 2L/c. |
Les exemple précédents sont repris ci-après en supposant la corde fixe à ses deux extrémités.
IV.3.3.b.
Exemple :
Vitesse initiale nulle
Pour cet exemple, nous avons supposé que la déformation initiale n’était pas imposée au milieu de la corde, mais vers une extrémité. On retrouve, pour les deux déformations crées à t=0: A et B, le comportement vis-à-vis des extrémités de la corde déjà identifié au $3.2.2. La fonction x étant linéaire en F et G, les deux perturbations s’ajoutent lorsqu’elle se rencontrent. Cela conduit périodiquement à retrouver la perturbation d’origine, mais aussi, pour des temps multiples de la demi-période, la déformation inverse par rapport au milieu de la corde.
Sur la figure 4.9, on a représenté pour le même cas le champ des vitesses (voir IV.7.3 page 40 ).
Figure IV‑9 : Corde fixée aux 2 extrémités
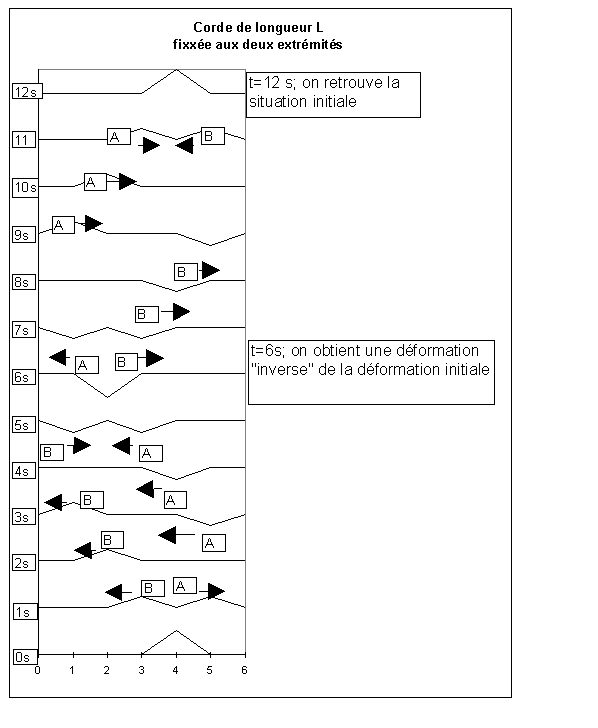
Figure IV‑10 : Vitesses sur une corde finie
(voir IV.7.5 page 44)
Le phénomène identifié sur le cas de la corde fixée simplement à une extrémité se retrouve ici aux deux extrémité: la vitesse est multipliée par 2 lors de la réflexion. On constate aussi que la corde retrouve une vitesse nulle pour les temps multiples d’une demi-période.
IV.3.3.c. Exemple : Vitesse initiale de la forme d’un Dirac
L’exemple du paragraphe 3.1.3 a été repris ici aussi avec une corde fixe aux deux extrémités. On constate les mêmes phénomènes de réflexion et de périodicité (voir IV.7.7 page 47).
Figure IV‑11 : Corde finie – Dirac en O
IV.3.4. Corde dont une des extrémité est libre
Il s’agit d’une situation proche de celle examinée au $3.2. On considérera ici que la corde se termine aussi en 0, mais que cette extrémité est libre verticalement. On peut imaginer cette extrémité liée à un anneau libre de coulisser sans frottement sur une tige verticale.
En 0, la corde ne subit aucune force provenant de sa partie « gauche »; en fait au point 0 la force transverse, du fait qu’il n’y a pas de masse ponctuelle, doit rester nulle quel que soit le temps t.
On a donc à rajouter au système d’équations (3), l’équation :
soit :
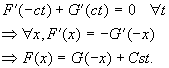
On retrouve une formulation analogue à l’équation (6) obtenue au chapitre 3.2, à la différence du signe - qui disparaît.
On en déduit donc que l’on observera un rebond en 0, comme dans le cas ou la corde était fixée, mais cette fois sans inversion de la déformation produite par l’onde. La formulation de la solution est donc la suivante:
|
|
(8)
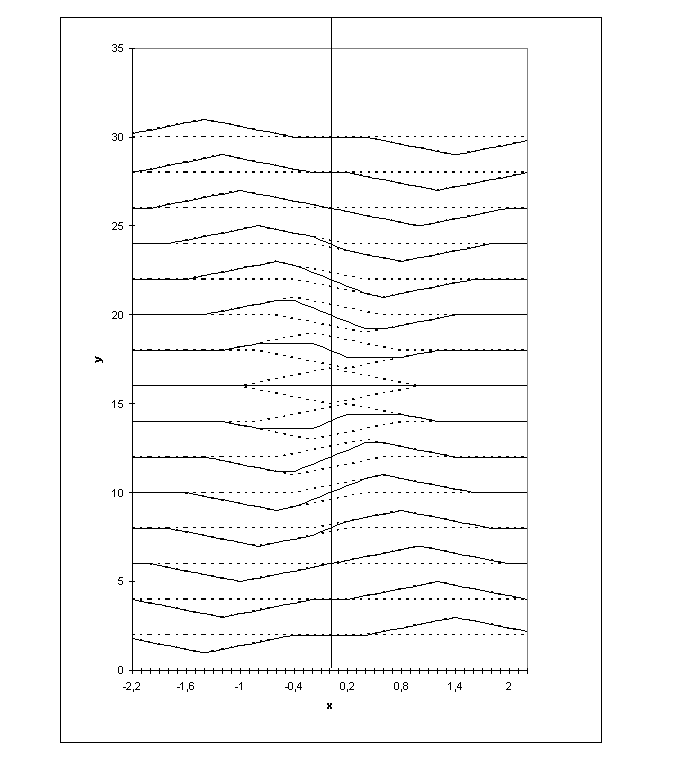
L’exemple du 3.2 a été repris et est illustré sur la figure ci-dessous dans le cas d’une extrémité libre (voir IV.7.9 page 50).
 |
Figure IV‑12 : Extrémité libre
IV.4. Propriétés des
solutions de l’equation des ondes
IV.4.1. Décomposition en fonctions périodiques pour une corde de longueur L
Sur une corde de longueur L, la solution
u(x,t), étant périodique (période= 2L/c soit 2Lr/T) peut être décomposée sur une base orthonormée constituée par les
fonctions 
; on peut alors écrire:
Pour déterminer les coefficients a dépendant de k (et de t), comme la base est orthogonale il suffit d’écrire:
(on pourra en trouver une démonstration précise au chapitre 5).
Pour déterminer a, il faut arriver à séparer sous le signe intégral les fonctions de x et de t; pour cela on utilise l’équation (1) en écrivant:
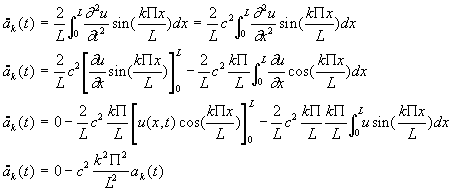
a vérifie donc l’équation :
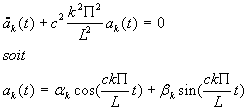
et enfin :
|
|
(9)
IV.4.2. Energie vibratoire
L’énergie de la corde en vibration E(t) doit être constante en fonction du temps si aucun effort extérieur n’est appliqué à la corde.
Cette énergie est la somme de l’énergie potentielle de la corde déformée et tendue, et de l’énergie cinétique de la corde.
L’énergie cinétique de la corde, Ec(t) est de manière évidente donnée par l’expression:
(10)
L’énergie potentielle va être définie au $ 4.2.1 et au $4.2.2 on vérifiera que E est bien constant en fonction de t.
IV.4.2.a.
Calcul de
l’énergie potentielle de la corde
On connaît la forme de la corde u(x,t) à l’instant t, et on veut calculer son énergie potentielle pour une solution u d’énergie finie.
Pour cela il faut déterminer l’apport d’énergie qui a été nécessaire pour amener la corde dans cet état. On supposera qu’il n’y a pas de dissipation thermique d’énergie.
Soit Ep(t) l’énergie potentielle de la corde définie par u(x,t).
On va calculer Ep(t) en supposant
que la corde est amené dans l’état u(x,t) à partir d’un état d’énergie nulle
(pour chaque x u est nul) par l’intermédiaire des états 
tels que:
a variant de 0 à 1.
Le travail des forces intérieures, W, est alors définie par l’équation suivante (voir les notations du $1):
pour une variation de da de a, le point d’application de la force 
dx se déplace de dau, donc:
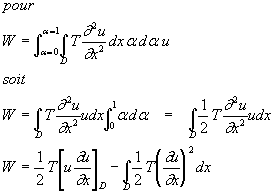
D étant le domaine de définition de u, il est
clair qu’aux bornes de D, l’expression 
ne peut être que
nulle.
Supposons en effet que la corde soit infinie,
pour une solution d’énergie finie il est clair que 
doit s’annuler à
l’infinie (de façon à ce que l’énergie cinétique soit finie), il en est donc de
même pour 
d’après (2).
Si la corde a une extrémité, sur cette
extrémité soit u est nul (
), soit la force qui s’y exerce est nulle(
), et donc l’expression u 
est encore nulle aux
extrémités. On a donc :
|
|
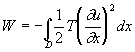
soit
(11)
IV.4.2.b.
Calcul de
l’énergie totale
L’énergie totale est alors définie en fonction du temps par:
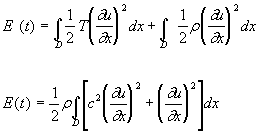
Calculons maintenant la dérivée de E par rapport à t:
or 
donc
d’après les considérations qui précèdent au sujet de u et de ses dérivées aux bornes de D.
E est donc constant en fonction du temps; on retrouve bien le premier principe de la thermodynamique.
La somme de l’énergie potentielle et de l’énergie cinétique de la corde est constante en fonction du temps en l’absence de forces extérieures.
IV.4.2.c.
Calcul de
l’énergie pour une corde de longueur finie
Dans le cas ou la corde a une longueur finie, on peut exprimer u(x,t) par l’expression (9), et on peut donc essayer de calculer E.
Calculons d’abord l’énergie potentielle:
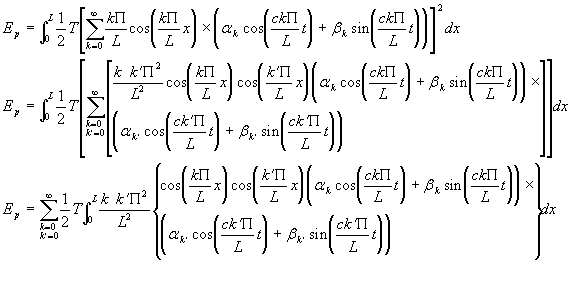
Mais comme la suite des fonctions 
est une base
orthogonale des fonctions sur [0,L], les intégrales ci-dessus sont nulles si k
est différent de k’ (on en verra une démonstration « à la main » dans
le chapitre 5). On a donc:
L’énergie cinétique elle peut être calculée comme suit :
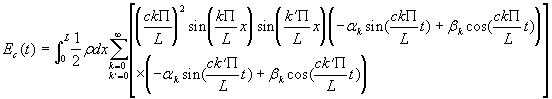
Comme précédemment, il ne reste que les termes pour lesquels k = k’; on a donc:
Comme 
, on a :
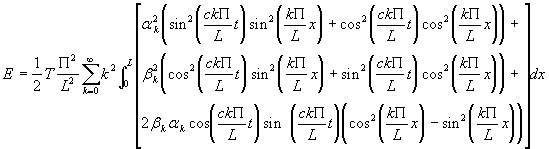
En utilisant la relation 
, on obtient :
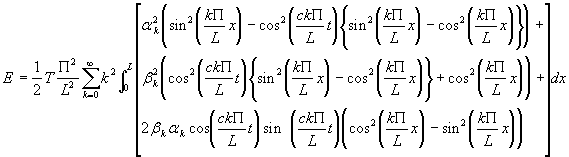
or : 
, on a donc :
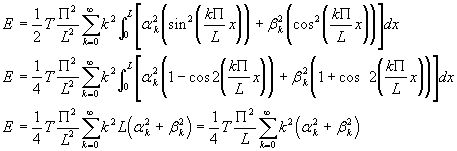
qui est bien indépendant de t, et est homogène à des N.m .
|
|
(12)
IV.5.
cas ou la corde est soumise à une force extérieure
IV.5.1.
Equation générale
L’équation (1) obtenue dans le cas ou la corde n’était soumise à aucune force extérieure est modifiée comme suit quand on suppose que la corde est soumise à une force répartie transverse définie par f(x,t):
|
|
(12)
Dans le cas général, la solution « générale » obtenue au §2 ne peut s’appliquer, car on aura :
(13)
et non pas 0.
Par contre dans le cas ou la force est localisée en un point, c’est à dire ou f est définie comme :
alors l’équation (13) est nulle en tout point sauf en 0.
On pourra alors utiliser la solution générale (2) pour x différent de 0:
(2) 
Ce sera le cas dans les paragraphes qui suivent.
IV.5.2.
Corde ayant une extrémité dont le
déplacement est imposé.
IV.5.2.a.
Corde infinie
Considérons le cas ou l’extrémité « gauche » de la corde est soumise à un mouvement défini par y(0,t)=m(t).
On va supposer aussi qu’a l’instant 0, la
corde est au repos (y(x,0)=0 et 
.
Le système d’équation (3) devient :
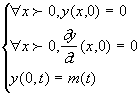
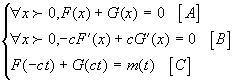
mais 
et 
entraînent que 
donc que 
.
On a donc d’après 
, 
Il reste donc à définir F pour x inférieur ou
égale à 0. Pour cela on utilise l’équation 
:
On a donc le résultat suivant:
|
|
Le mouvement du point 0 se propage donc sur la corde à la vitesse c.
La figure 4.13 ci-après illustre le phénomène quant m(t)=sin(5t)/2
Figure
IV‑13 : Mouvement
de l’origine fixée
|
|
Pour cet exemple, on peut facilement calculer la force nécessaire qu’il faut appliquer à l’origine pour maintenir le mouvement:
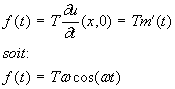
L’accélération du point 0 étant 
, on peut considérer que la corde attribue au point 0 une
masse « fictive » égale à : 
.
IV.5.2.b.
Corde finie de
longueur L
IV.5.2.b.i. Solution générale
Par rapport au cas précédent ou on créait une onde se propageant vers la droite, dans ce cas-ci, après une première phase de propagation vers la droite, l’onde va repartir vers la gauche après avoir atteint l’extrémité droite; elle se superposera alors à l’onde qui continue à arriver de la gauche. Quant elle aura atteint l’extrémité gauche, elle se réfléchira sur celle-ci et repartira vers la droite. Le mouvement résultant sera alors une superposition de n ondes (n étant le nombre de fois ou l’onde c’est réfléchie sur une extrémité) dont la phase par rapport à l’onde initiale dépendra de la longueur L de la corde, en fait de L/c.
Le système initial s’écrie alors :
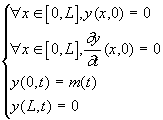
soit :
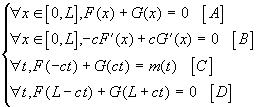
Comme précédemment on déduit de ce système :
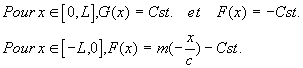
De l’équation [D], on déduit G pour les x du segment [L,2L] :
on considère t tel que 
, alors :
on considère maintenant t tel que 
, et avec [C] on obtient :
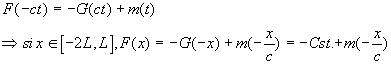
On a donc pour F:
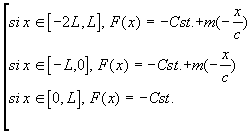
et pour G:
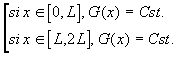
On obtient G entre 2L et 3L en utilisant encore [D]:
pour ct dans le segment [L,2L], on a :
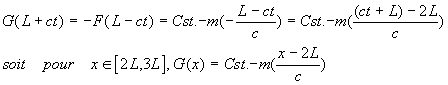
On en déduit immédiatement grâce à [C] : 
On vérifiera facilement par récurrence que :
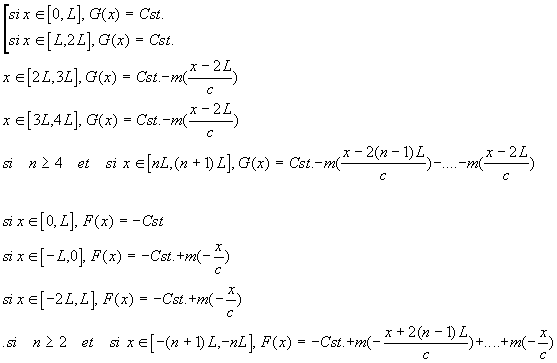
IV.5.2.b.ii. Solution particulière (exemple)
Supposons que m(t)=Asinwt, on a alors:
on peut considérer F comme étant la partie imaginaire de l’expression:
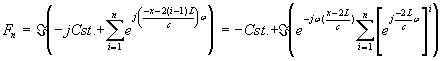
soit
si 
c’est à dire si 
:
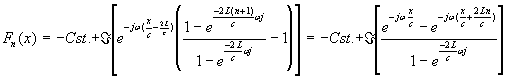
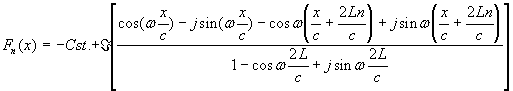
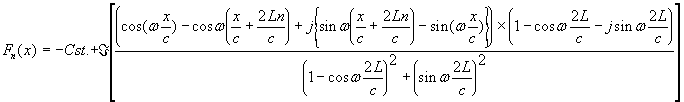
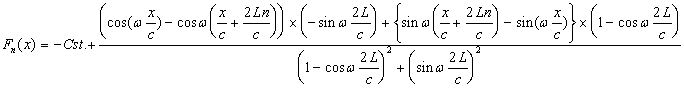
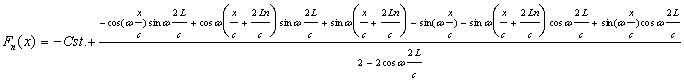
mais:
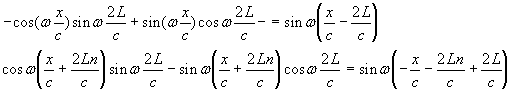
donc:
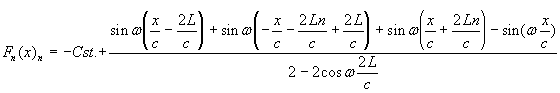
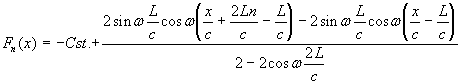
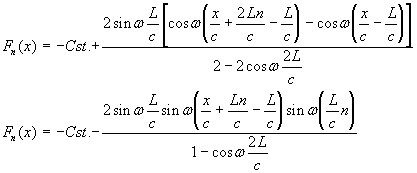
On a donc :
|
|
Et pour G, on peut écrire :
on obtient donc G à partir de l’expression
donnant F en remplaçant x par -x dans le terme 
, soit :
|
|
Il nous reste maintenant à établir l’expression de u(x,t).
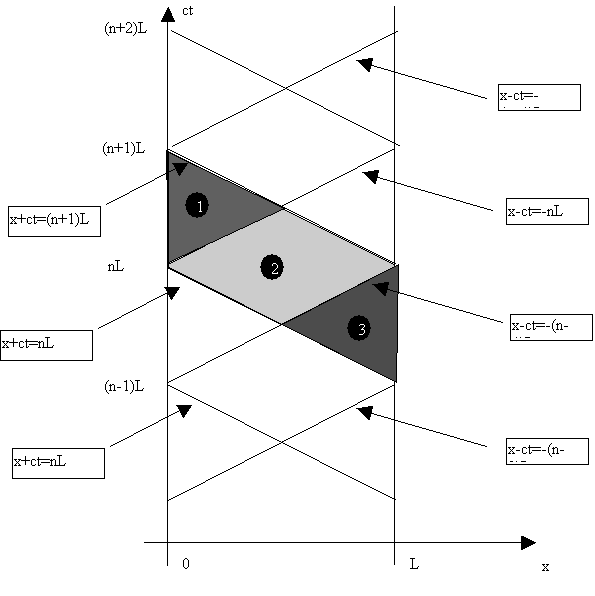
Pour cela considérons x et t tels que (x+ct)Î[nL,(n+1)L], alors on a (voir figure 4. ci-après):
-(n+1)L < -x-ct < -nL mais comme 0 < x < L, on a : -(n+1)L < x-ct < -(n-2)L, soit trois possibilités :
¶
-(n+1)L<x-ct<-nL è 
·
-(n)L<x-ct<-(n-1)L è 
¸
-(n-1)L<x-ct<-(n-2)L è 
Figure IV‑14
Supposons que 
, alors:
¶ donne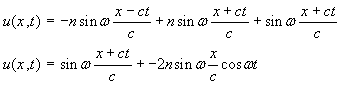 
· donne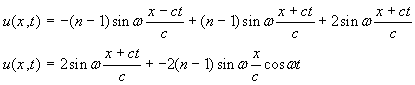 
¸ donne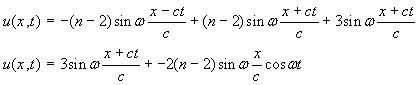 
On passe de ¶ à · quand x-ct=-nl, sur la frontière on doit avoir ¶ = ·, ce qui est évident en écrivant
alors que 
=0.
Les expressions obtenues montrent que
l’amplitude croit comme n, et donc tend vers l’infinie quant t tend vers
l’infini; il y a résonance.
En fait la condition 
entraîne que quand un
onde se réfléchie sur un extrémité, l’onde qui repart en sens inverse s’ajoute
à l’onde qui continue à arriver de l’autre extrémité.
On notera de plus, qu’au premier ordre prés, la forme de la corde est obtenue par le produit d’une fonction du temps et d’une fonction spatiale.
Concrètement, 
, est la période de la sollicitation imposée à la corde,
il y a résonance quand cette période est multiple de 
,
qui est la période « propre » de la corde vue au §IV.3.3.a.
Maintenant
examinons le cas ou 
On a donc dans le cas ¶ :
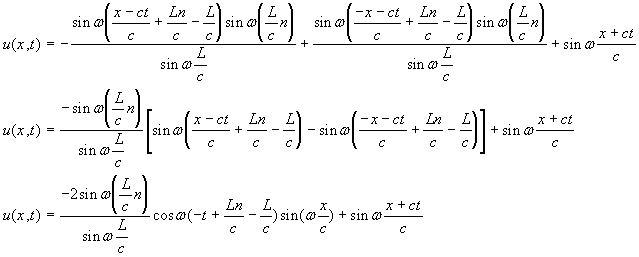
On retrouve une expression équivalente à celle
obtenue précédemment quant il y avait résonance, on trouve en effet que le
résultat est la somme de la fonction 
et d’un produit d’une
fonction temporelle par une fonction spatiale; mais cette fois sans
convergence.
Le calcul n’a été fait que pour le cas ¶, mais on trouverait le même résultat pour les deux autres.
IV.6. Conclusion pour
les cordes finies
Pour les cordes de longueur finie L, de tension T et de masse linéaire r :
Ces cordes peuvent
conduire qu’à des vibrations de fréquences multiples de 
,
Si une telle corde est
excitée par une vibration dont la période est multiple de la sienne, alors elle
rentre en résonance.
IV.7. TABLE des ANNEXES
|
1 |
Positions |
Triangle |
Corde infinie |
|
2 |
Positions |
triangle |
Corde fixée à une extrémité |
|
3 |
positions |
Triangle |
Corde finie |
|
4 |
Vitesses |
Triangle |
Corde fixée à une extrémité |
|
5 |
Vitesses |
triangle |
Corde finie |
|
6 |
Positions |
Dirac en vitesse |
Corde infinie |
|
7 |
Positions |
Dirac en vitesse |
Corde finie |
|
8 |
Positions |
Triangle |
Corde infinie, simulation du rebond sur l’extrémité fixe d’une corde |
|
9 |
Positions |
Triangle |
Corde ayant une xtrémité libre |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
IV.7.1.
Annexe 1 : Corde infinie
IV.7.2. Annexe 2 : Positions pour une corde fixée à une seule extrémité
IV.7.3.
Annexe 3 : Positions pour une
corde fixée aux deux extrémités
IV.7.4.
Annexe 4 : Vitesses pour une
corde fixée à une extrémité
IV.7.5.
Annexe 5 : Vitesses pour corde
fixée aux deux extrémités
IV.7.6.
Annexe 6 : Corde infinie – Dirac
en vitesse
IV.7.7.
Annexe 7 : Positions pour une
corde fixée aux deux extrémités – dirac en vitesse à 0
IV.7.8.
Annexe 8 : Simulation d’une corde
fixée à une seule extrémité par une corde infinie
IV.7.9.
Annexe 9 : Positions pour une
corde fixée à une seule extrémité
