Chapitre III. Calcul des fréquences des notes Définition des « tons »
Dans ce chapitre suite aux définitions données dans le chapitre 1 sur le nom des notes, sur leurs principales caractéristiques et sur les gammes usuelles, nous allons définir précisément pour chaque note de la gamme sa fréquence absolue, prenant en compte comme référence que le La3 a une fréquence de 440 Hertz. Nous définirons aussi l’échelle des tons.
Chapitre III. Calcul des
fréquences des notes Définition des « tons »
III.1. Définition « mathématique » des « tons »
III.2. Calcul des fréquences des notes
III.1.
Définition « mathématique » des
« tons »
On a vu que l’on définissait une octave comme l’intervalle séparant une note de la note de même nom immédiatement supérieure ou inférieure. En fait, si la fréquence de cette note N, est F(N), l’octave mesure la différence entre 2n*F(N) et 2(n+1)*F(N) ou n est un entier relatif (n pouvant être négatif).
L’écart , ET(N1, N2) entre deux notes, N1 et N2, doit mesurer la différence entre les « hauteurs » des notes ayant comme fréquences :
F(N2) et F(N1).
Cet écart doit être constant quelle que soit l’octave, c’est à dire:
ET(N1, N2) = HN(N1) - HN(N2) = ET(N1n, N2n) = HN(N1n) - HN(N2n) quel que soit n entier relatif,
avec N1n la note de même nom que N1 et telle que F(N1n)=2n*F(N1).
Définissons H(F1)=HN(N1) avec F1 = F(N1), H sera appelée « hauteur » de N1.
Nous cherchons à définir H pour que ce soit une fonction C¥ sur son domaine de définition et croissante.
H vérifie déjà:
V nÎQ, H(2n*F2) - H(2n*F1) = H(F2) - H(F1) (1)
Cette définition ne suffit pas à déterminer H de manière unique, en effet, on pourrait définir H sur [1,2] de façon quelconque en assurant que les dérivées successives de H à gauche de 1 soient égales aux dérivées successives à droite de 2, et en définissant pour tout x, x>0, F(x) en considérant l’entier n, tel que xÎ[2n,2n+1], et en écrivant que H(x) = H(x/2n) + n. On vérifiera aisément qu’une telle fonction vérifie l’équation (1).
Pour définir de manière non ambiguë la fonction H, il faut rajouter des contraintes à l’équation (1). Pour cela on va se servir des observations du chapitre 1.2 concernant la façon d’obtenir une échelle de notes à l’aide de cordes vibrantes de longueurs différentes.
On a en effet vu que si pour une corde de longueur L, le son émis est un Do, la corde de longueur 2/3*L émettra un Sol. L’écart entre ces deux notes est ensuite égal quelle que soit l’octave considérée. On peut élargir cette propriété en considérant que ce qui différencie alors ces notes est le rapport des fréquences des sons émis. On peut alors chercher à définir H, en imposant que quelles que soient deux fréquences ayant un rapport donné, l’écart entre les hauteurs de ces deux fréquences soit constant. Si on reprend l’exemple de la corde ci-dessus, cela revient à dire que l’on cherche H telle que si deux fréquences sont dans le rapport 3/2, alors la différence des hauteurs est égale à la différence des hauteurs de Sol et Do.
Cela s’écrie,
V qÎR, V F1,F2 ÎR, on a H(qF1) - H(F1) = H(qF2) - H(F2) (2)
En fait cette relation s’écrie aussi :
V qÎR : H(qF2)-H(qF1) = H(F2) - H(F1) (3)
ce qui correspond à une généralisation de la relation (1).
On va chercher à définir les fonctions H vérifiant (3).
Cherchons à définir sa dérivée:
H’(F) = ![]()
d’après (3) on a:
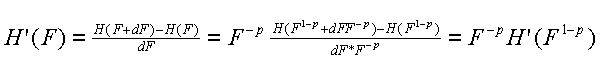
et ce ![]()
c’est donc vrai pour p=1 et donc
|
|
On en déduit immédiatement que H(F) = Log(C*F) ou C= H’(1)
|
H(F)
= Log(C * F) |
l’écart entre deux notes est donc N1 et N2, est donc égal à :
|
Log(C*F(N2)) - Log(C*F(N1)) |
L’écart correspondant à une octave, est alors Log(2)
et est indépendant de l’octave considérée (et de la note prise en compte pour définir l’octave).
Si maintenant on veut mesurer l’écart entre deux notes en l’exprimant en tons, chaque tons étant un douzième de l’octave, cet écart s’écrit:
|
ET(N1, N2) = 12/Log(2) * ( Log(F(N2))
- Log(F(N1) ) |
(5)
III.2.
Calcul des fréquences des notes
A partir de la formule (5) , si on connaît la fréquence d’une note de référence , N0 , et l’écart séparant les autres notes de cette note de référence, on peut calculer la fréquence des notes par:
|
Log(F(N1)) =
Log(F(N0) + Log(2)/12 * ET(N0, N1) |
(6)
La note de référence choisie a été historiquement le La3 pour laquelle la fréquence a été fixée à 440 Hertz.
On peut donc aisément calculer les fréquences des notes de la gamme diatonique majeure en sachant que les écarts en ton entre chacune des notes sont les suivants:
|
Note |
Ecarts |
|
Do |
2 |
|
Ré |
2 |
|
Mi |
1 |
|
Fa |
2 |
|
Sol |
2 |
|
La |
2 |
|
Si |
1 |
De plus l’écart séparant une note de son altération, # ou b est toujours de 1 ton (# = + ½ ton; b = - ½ ton); du moins quand on pratique la technique d’accord dite à tempérament égal.
Les fréquences des notes sont alors données dans le tableau T2-1, et représentées sur les figures F2-1 et F2-2.
On pourra vérifier que ces fréquences respectent à peu prés les rapports définis au chapitre 1 sur la figure 1-5.
Tableau 2-1
|
Do1 |
65,41 |
Do2 |
130,81 |
Do3 |
261,63 |
Do4 |
523,25 |
Do5 |
1046,50 |
Do6 |
2093,00 |
|
Do#1 |
69,30 |
Do#2 |
138,59 |
Do#3 |
277,18 |
Do#4 |
554,37 |
Do#5 |
1108,73 |
Do#6 |
2217,46 |
|
Re1 |
73,42 |
Re2 |
146,83 |
Re3 |
293,66 |
Re4 |
587,33 |
Re5 |
1174,66 |
Re6 |
2349,32 |
|
Re#1 |
77,78 |
Re#2 |
155,56 |
Re#3 |
311,13 |
Re#4 |
622,25 |
Re#5 |
1244,51 |
Re#6 |
2489,02 |
|
Mi1 |
82,41 |
Mi2 |
164,81 |
Mi3 |
329,63 |
Mi4 |
659,26 |
Mi5 |
1318,51 |
Mi6 |
2637,02 |
|
Fa1 |
87,31 |
Fa2 |
174,61 |
Fa3 |
349,23 |
Fa4 |
698,46 |
Fa5 |
1396,91 |
Fa6 |
2793,83 |
|
Fa#1 |
92,50 |
Fa#2 |
185,00 |
Fa#3 |
369,99 |
Fa#4 |
739,99 |
Fa#5 |
1479,98 |
Fa#6 |
2959,96 |
|
Sol1 |
98,00 |
Sol2 |
196,00 |
Sol3 |
392,00 |
Sol4 |
783,99 |
Sol5 |
1567,98 |
Sol6 |
3135,96 |
|
Sol#1 |
103,83 |
Sol#2 |
207,65 |
Sol#3 |
415,30 |
Sol#4 |
830,61 |
Sol#5 |
1661,22 |
Sol#6 |
3322,44 |
|
La1 |
110,00 |
La2 |
220,00 |
La3 |
440,00 |
La4 |
880,00 |
La5 |
1760,00 |
La6 |
3520,00 |
|
La#1 |
116,54 |
La#2 |
233,08 |
La#3 |
466,16 |
La#4 |
932,33 |
La#5 |
1864,66 |
La#6 |
3729,31 |
|
Si1 |
123,47 |
Si2 |
246,94 |
Si3 |
493,88 |
Si4 |
987,77 |
Si5 |
1975,53 |
Si6 |
3951,07 |
On peut aussi écrire (3) de la façon suivante:
|
F(N1) = F(N0) * 2 (ET(N0,N1)/12) |
(4)
L’écart entre deux notes mesure donc le logarithme base 2 du rapport des fréquences de ces notes.
Du tableau 2-1, on peut tirer que F(Do0) est proche de 32 Hertz, ce qui correspond à 25.
Si on représente une note N, donnée par un couple (x,y), ou x représente le numéro de l’octave, et y, le nombre de demi-tons entre cette note et le Do de la même octave, on peut écrire:
|
F(N) = 2 (5+x+y/12) |
(5)
Et enfin, on peut aussi définir une « hauteur » absolue d’une note en la définissant comme étant le logarithme base 2 de sa fréquence. Pour une note (x,y), la hauteur serait donc 5+x+y.
Exemple : La formule (5) donne pour le La3 la valeur de 2(5+2+9/12) = 430,5 Hertz, ce qui est très proche de la valeur de référence de 440 Hertz.
De toute façon, la fréquence absolue d’une note n’a que peu d’importance, seul les écarts entre les notes sont importants. La fréquence absolue sert à « accorder » plusieurs instruments entre eux sans qu’il soit nécessaire de le faire en même temps pour tout les instruments.
III.3.
Tempérament non égal
Si on définit les notes en considèrent les ½ tons diatoniques et chromatiques, c’est à dire respectivement 4/9 et 5/9 d’un ton, on rajoute une note entre deux notes comme ci-après: N1 N#1 Nb2 N2
Par exemple si on prend le Do1 comme point de départ, on :
à tempérament égal : Do1 = 65,4 Hertz Do#1= Ré b1 = 69,3 Hertz Ré1 = 73,4 Hertz
sinon : Do1
= 65,4 Hertz Do#1=
68,8 Hertz Ré b1= 69,7
Hertz Ré1 =
73,4 Hertz
Figure III‑1 : Fréquence
des notes
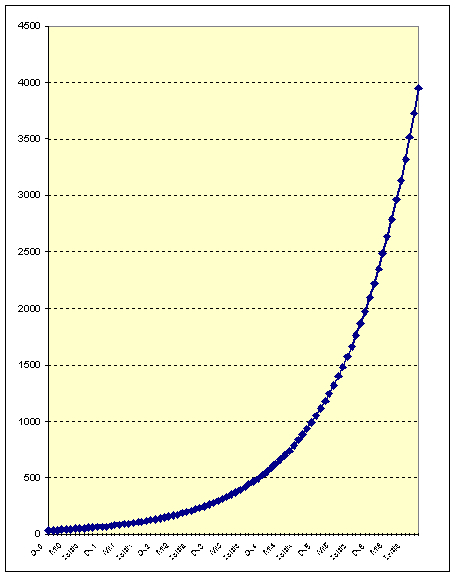
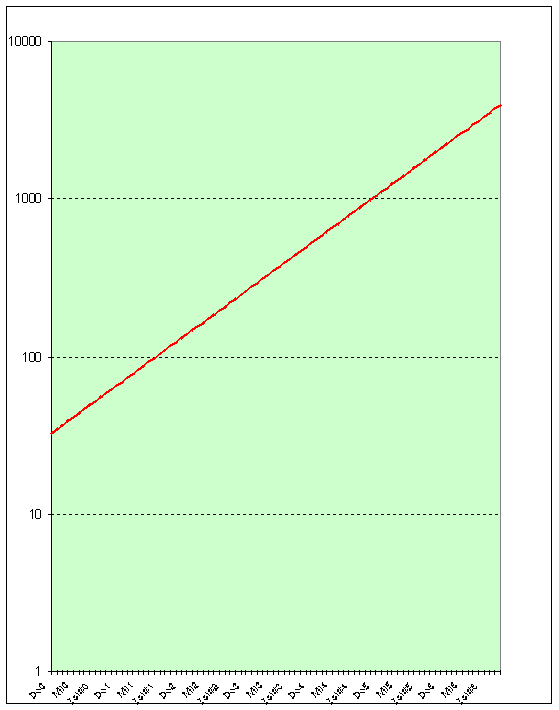
Figure III‑2 : Fréquences
des notes (échelle logarithmique)
III.4.
Liste des figures
Figure III‑1 : Fréquence des notes
Figure
III‑2 : Fréquences des notes (échelle logarithmique)
III.5.
Références
[1] : Encyclopédie Universalis : « Musique contemporaine »
[2] : Encyclopédie Universalis : « Acoustique : propagation des sons »
[3] :
Neville H. FLETCHER et Thomas D. ROSSING ¤ « The physics of musical
instruments » ¤ Springer-Verlag
[4] : A. DANHAUSER ¤ « Théorie de la musique » ¤ 1995 ¤ Editions Henry lemoine
[5] : Encyclopédie CLARTE ¤ Tome « Loisirs » ¤ La musique
[6] : QUID 1997 : « Notation Musicale »
[7] : J.L. Armand ¤ « Dynamique des structures « ¤ ENSTA 1984
[8] : P. Germain ¤ « Cours de mécanique « ¤ Ecole Polytechnique 1982
[9] : Y. Meyer ¤ « Analyse Hilbertienne » ¤ Ecole Polytechnique 1982
[10] : J.L. Lions ¤ « Cours d’analyse numérique » ¤ Ecole Polytechnique 1982
[11] : G. Goulaouic « Analyse factorielle et calcul différentiel » ¤ Ecole Polytechnique 1982
[12] : Nouveau Larousse illustré ¤ 1906 ¤ « Musique »
[13] : Encyclopédie CLARTE ¤ Tome Beaux arts II ¤ « Histoire de la musique »
[14] : Encyclopédie CLARTE ¤ Tome Lois de la vie I ¤ « La perception des sons »
[15] : J. Duc et D. Bellet ¤ Mécanique des solides réels - Elasticité ¤ Ecole nationale supérieure de l’aéronautique et de l’espace
[16] :
Raymond J. Roark & Warre G. Young ¤ Formula for stress and strain ¤ Mc.
Graw Hill Book Company
[17] : G. Pissarenko - A. Yakovlev - V. Matveev ¤ Aide mémoire de résistance des matériaux ¤ Editions MIR
[18] : Paul Beuscher ¤ Guitar Digest ¤ Editions Paul Beuscher