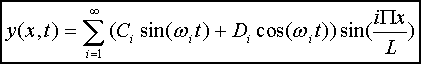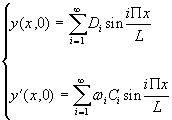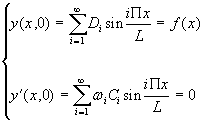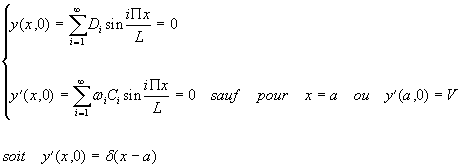Chapitre V. Les mouvements d’une corde vibrante
Dans ce chapitre, on va « visualiser » les mouvements d’une
corde vibrante sur deux exemples, les cordes pincées et les cordes frappées, respectivement
principe de la guitare et principe du piano.
Chapitre V. Les mouvements
d’une corde vibrante
V.1. Equation
générale du Mouvement
V.2.2. Résolution de
l’équation du mouvement
V.3.2. Résolution de
l’équation du mouvement
V.1. Equation générale du Mouvement
Dans le chapitre 4, on a vu que l’équation générale du mouvement d’une
corde vibrante de longueur L, de tension T et de masse linéaire r était la suivante :
|
|
(1)
avec ![]() et
et 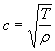
Ci et Di
étant définis en fonction des conditions à t=0.
A t=0, les déplacements et vitesses sont donnés par:
|
|
(2)
V.2. Cas d’une corde pincee
V.2.1. Définition
Une corde pincée est une corde que l’on excite en la déformant par
déplacement d’un de ces points jusqu’à une position d’équilibre, et que l’on
relâche instantanément. La corde déformée a ainsi la forme suivante:
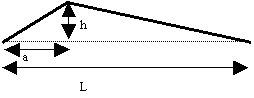
A l’instant t= 0, on a donc sur [0,L]:
|
|
(3)
V.2.2. Résolution de l’équation du mouvement
Si on multiplie par ![]() chaque équation de (3)et si on intègre de 0 à L, on
obtient :
chaque équation de (3)et si on intègre de 0 à L, on
obtient :
(4) 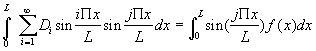
et
(5) 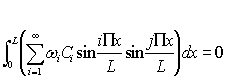
De (5), on tire :
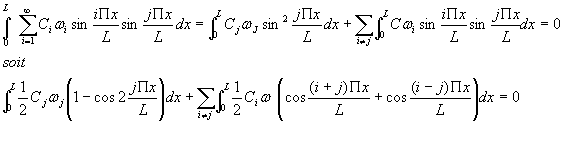
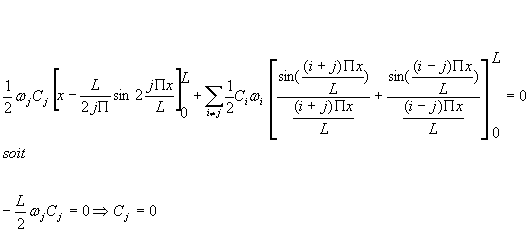
|
On a donc Cj = 0 quel que soit j. |
De (4) on tire :
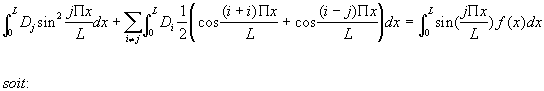
|
|
(6)
(6) se résout de la manière
suivante en utilisant la démarche vue pour résoudre (4):
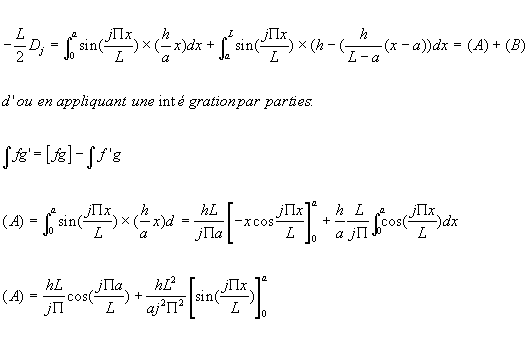
![]()
et avec (B) :
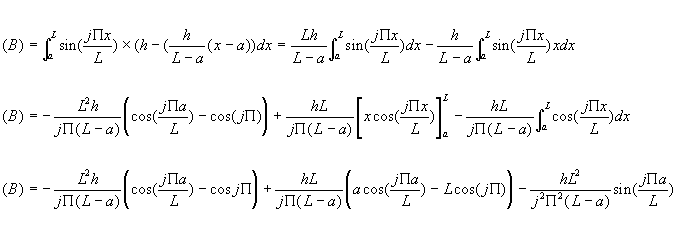
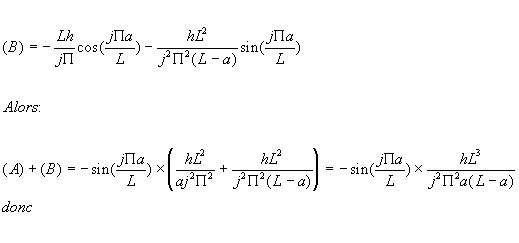
|
|
On en déduit deux propriétés immédiates :
- Dj , qui
est l’amplitude de l’harmonique j, décroît comme l’inverse du carré de j; le
son résultant sera donc proche du fondamental
- Dj s’annule pour ![]() , avec m=
0,1,2,3,...,n,...
, avec m=
0,1,2,3,...,n,...
On perd ainsi toutes les harmoniques qui auraient présenté un nœud en
a. Par exemple si on pince la corde en son milieu, on perd toutes les
harmoniques paires.
V.2.3. Visualisation
Pour visualiser le mouvement de la corde, nous allons prendre une corde
dont les caractéristiques sont les suivantes:
Longueur = L = 1 m
Tension = T = 100 N
Masse linéaire = r = ![]()
r est calculé en supposant que la corde est en acier, et a un diamètre
de 0,0002 m (deux dixième de millimètre); la masse volumique de l’acier est de
l’ordre de 8000 kg/m 3, la masse linéaire est alors de :
![]()
Avec ces données la vitesse de propagation de l’onde est de l’ordre de
630 m/s et la fréquence du son fondamental est de 315 Hertz, ce qui
correspondrait au Ré#3 . La période de la perturbation
est de 0,0032 secondes.
La forme de la corde à différents instants est donné sur les figures 5-1et
5-2 ci-après. Pour tracer ces figures nous n’avons pris en compte que 13
harmoniques. [à vérifier].
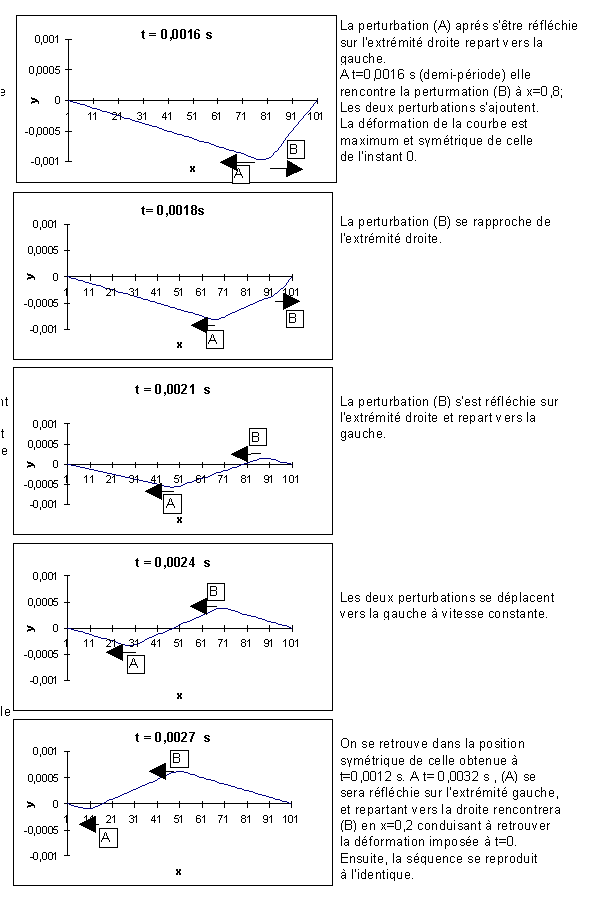
On constate bien que les perturbations se déplacent sur la corde à
vitesse constante et se réfléchissent aux extrémités.
Figure
5-1
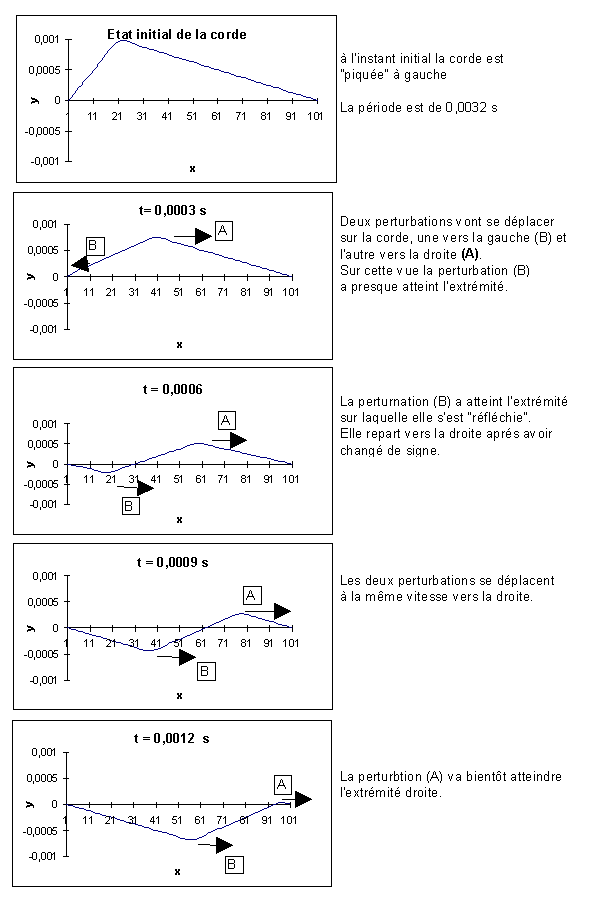
Figure 5-2
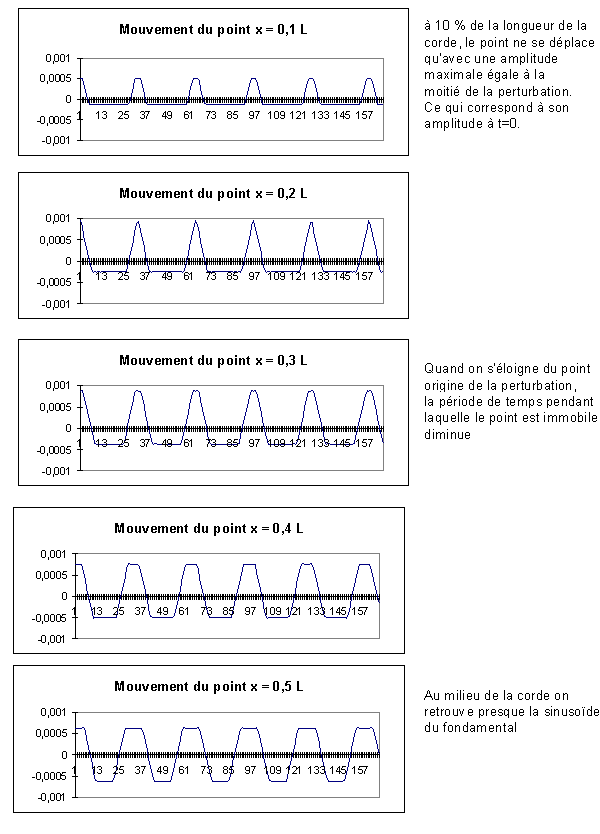
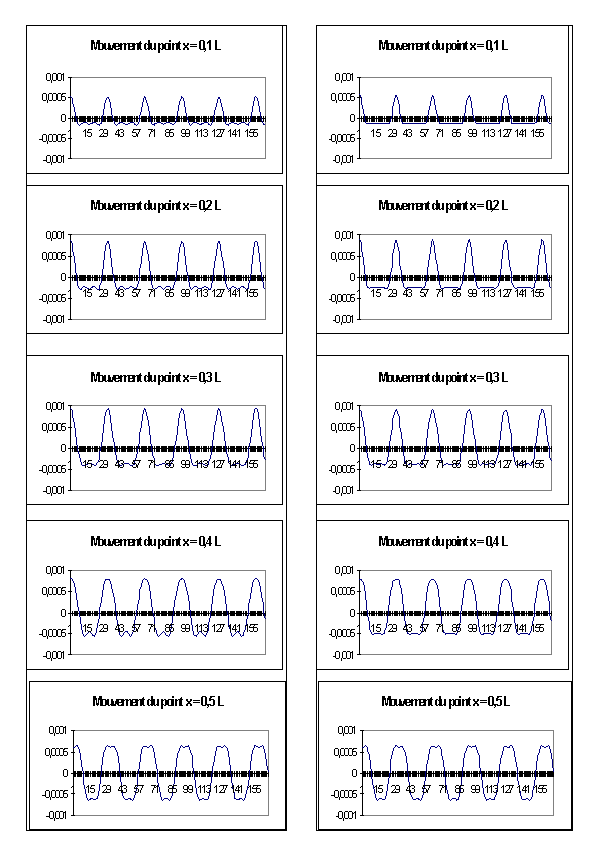
Il est aussi intéressant d’examiner les mouvements au court du temps de
certains points de la corde tels que représentés ci-dessous sur la figure 5-3.
Figure
5-3
On peut aussi représenter le mouvement de la corde en trois dimensions
pour visualiser les déformations de la corde en fonction du temps comme sur la
figure 5-4 ci-après.
Figure
5-4
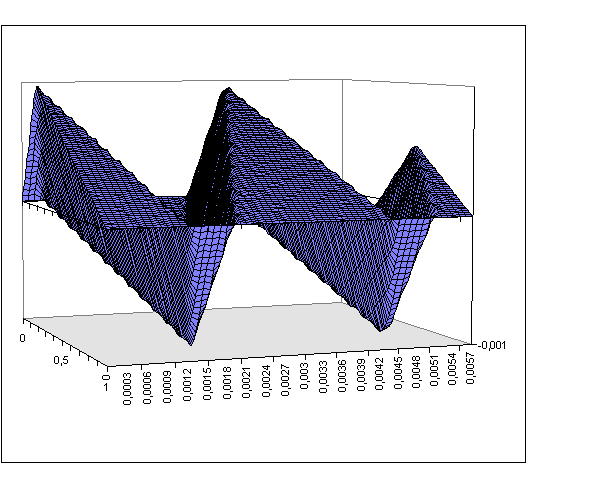
Ces différentes courbes illustrent bien le mouvement ondulatoire de la
corde en régime établi. On a néanmoins du mal à identifier les différentes
harmoniques tels que prévues par l’équation (1), particulièrement en ce qui concerne l’évolution de la forme de
la corde. Dans le paragraphe suivant on va tenter de visualiser l’effet de la
présence des harmoniques.
V.2.4. Effet des harmoniques
Nous avons repris le même problème que précédemment, mais en nous
limitant pour la représentation graphique aux contributions respectivement du
fondamental seul (cas ¶), du fondamental et de sa première harmonique - qui
est de fréquence double - (cas·), du fondamental et de ses
deux premières harmoniques (cas ¸) et du fondamental et des
ses trois premières harmoniques (cas¹).
On retrouve sur les figures suivantes les grandeurs représentées sur
les figures 5-1 à 5-3:
|
4-5 |
¶ et
· |
t = 0 ; t = 0,0003 s : t = 0,0006 s ; t = 0,0009 s t = 0,0012 s |
|
4-6 |
¶ et
· |
t = 0,0016 s ; t = 0,0018 s ; t = 0,0021 s t = 0,0024 s ; t = 0,0027 s |
|
4-7 |
¸ et
¹ |
t = 0 ; t = 0,0003 s : t = 0,0006 s ; t = 0,0009 s t = 0,0012 s |
|
4-8 |
¸ et
¹ |
t = 0,0016 s ; t = 0,0018 s ; t = 0,0021 s t = 0,0024 s ; t = 0,0027 s |
|
4-9 |
¶ et
· |
x = 0,1 ; x = 0,2
; x = 0,3 ; x = 0,4
; x = 0,5 |
|
4-10 |
¸ et
¹ |
x = 0,1 ; x = 0,2
; x = 0,3 ; x = 0,4
; x = 0,5 |
Examinons d’abord le cas ¶; ce cas correspond au
fondamental du son considéré, et la forme de la corde à chaque instant n’est
donnée que par une fonction cosinus dont l’amplitude elle même est une fonction
cosinus du temps; la forme de la corde est donc sinusoïdale quel que soit le
temps. Par contre, la forme de la corde, toujours symétrique par rapport à son
milieu, ne correspond pas du tout à l’instant 0 à la forme initiale de la corde
excitée. Pour obtenir la forme initiale, il va falloir lui ajouter des
corrections visant à corriger cette forme « fondamentale » de façon à
redonner à l’instant 0, mais aussi à tous les instant nT ou T est la période,
la forme de la corde excitée telle que présentée sur la figure de la page 1.
Ces corrections seront en fait les différentes harmoniques du son.
Le cas · par exemple,
présente la somme du son fondamental et du son correspondant à une fréquence
double. A l’instant 0, la forme qu’aurait la corde pour ce premier harmonique
seul correspondrait à une sinusoïde complète (c’est à dire sur une période).
Son premier maximum serait pour L=1/4, la déformation serait nulle à L=1/2 et
la déformation serait minimale (négative) pour L=3/4. La somme de cette
fonction au fondamental va donc « piquer » la courbe résultante vers
L=1/4; c’est ce que l’on observe sur la figure 4-5 par exemple.
Au fur et à mesure que l’on rajoute des harmoniques, on se rapproche à
l’instant 0 de la forme initiale de la courbe. Dans cet exemple, du fait que la
déformation initiale imposée n’est pas Cµ au point de cassure
de la courbe initiale, il faudra prendre en compte un nombre important
d’harmoniques pour obtenir cette discontinuité. Dans le cas « réel »,
il est clair que la corde ne présentera pas un tel point singulier à l’instant
initial, et que donc les harmoniques de rang élevé devraient voir leur
amplitude diminuer.
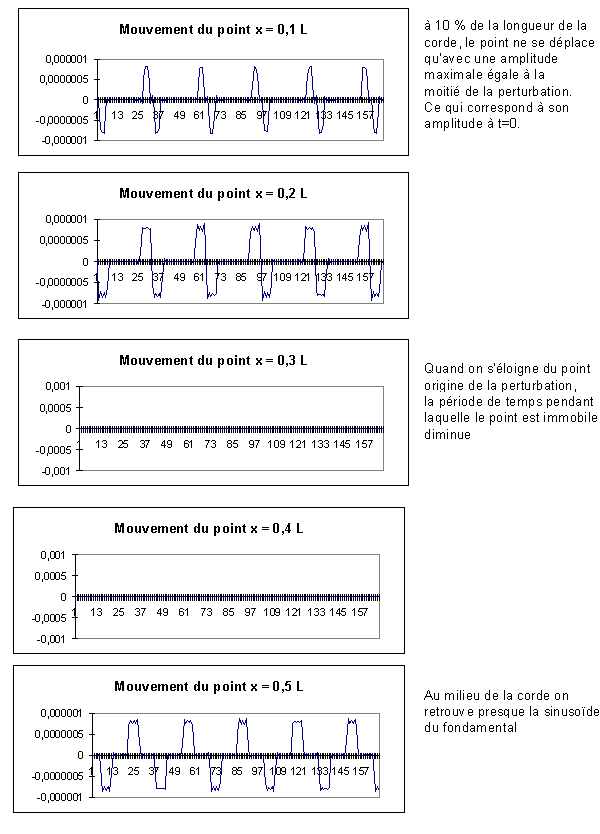
On constate le même phénomène sur les figures présentant les positions
en fonctions du temps de certains points de la courbe. Sans harmoniques on
retrouve ne sinusoïde. L’ajout d’harmoniques conduit, petit à petit, à
retrouver les plages de temps pendant lesquelles chaque point est immobile. Ces
zones « plates » sont construites par l’ajout de sinusoïdes dont la
fréquence augmente et l’amplitude diminue. On vérifiera par un rapide calcul
que les vitesses des points induites par chaque harmonique ne décroît qu’avec
le rang de l’harmonique (et non son carré), et que donc il serait nécessaire,
si l’on voulait représenter les courbes des vitesses des points considérés de
prendre en compte un nombre bien plus important d’harmoniques (ce que nous
n’avons pas fait ici du fait des capacités limitées de calcul à notre
disposition).
Le son ainsi perçu par l’oreille, ne ressemble pas du tout à un son que
l’on pourrait qualifier de pur, c’est à dire tel que celui qui serait émis par
une corde vibrant seulement selon son fondamental, mais une composition, un
mélange de tous les harmoniques.
Figure
5-5
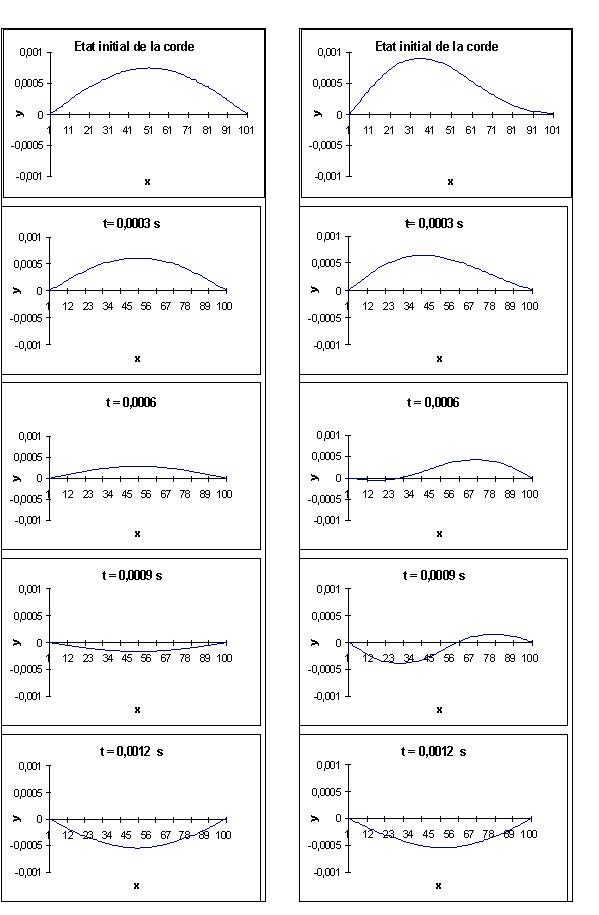
Figure 5-6
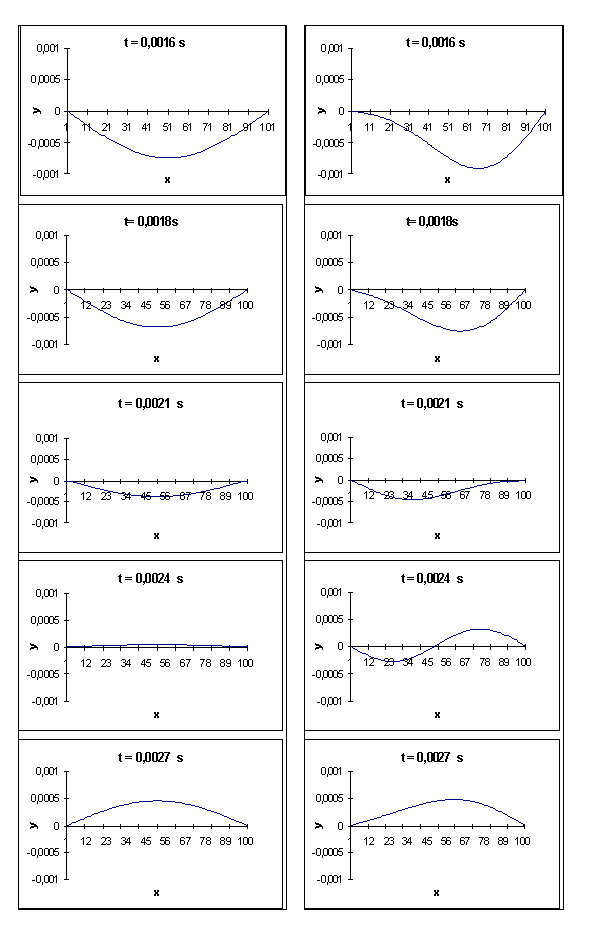
Figure 5-7
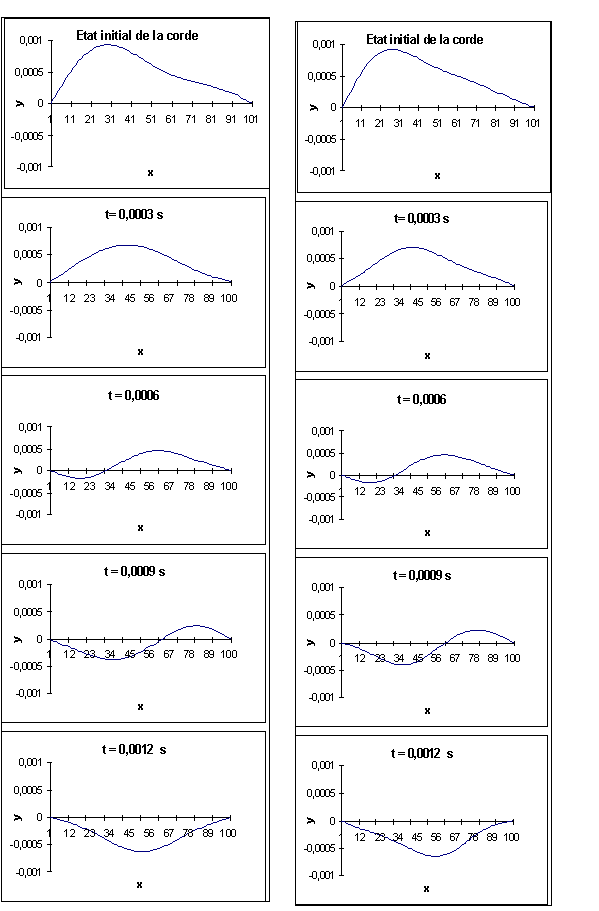
Figure 5-8
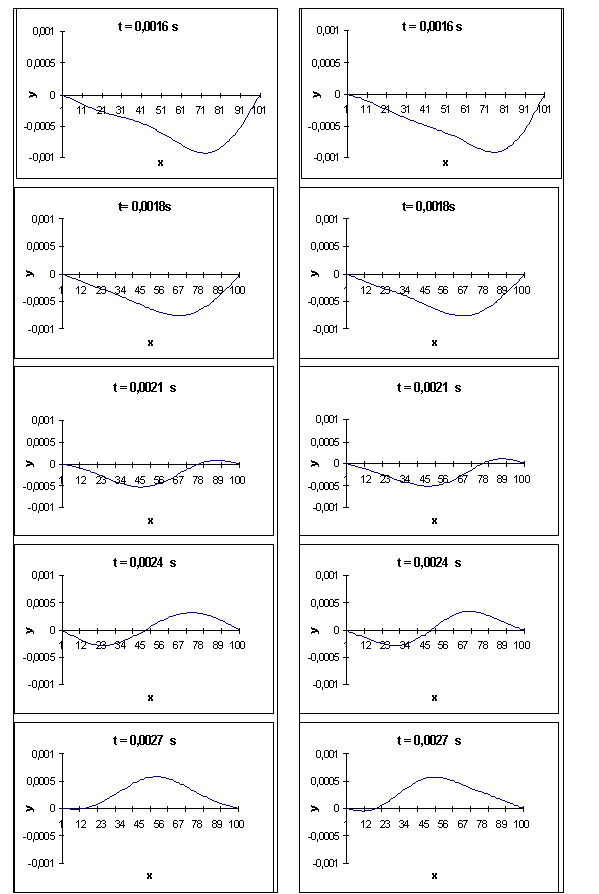
Figure 5-9
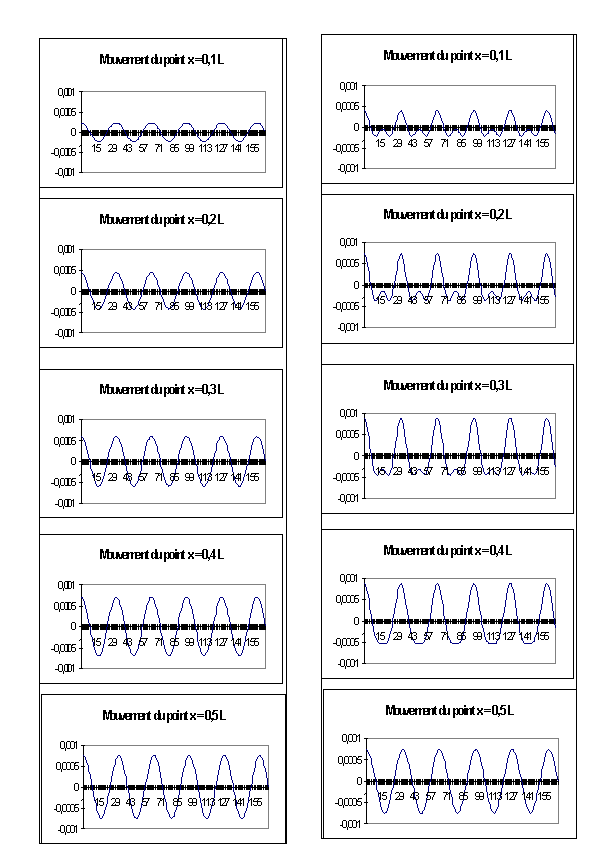
Figure 5-10
V.3. Cas d’une corde frappée
V.3.1. Définition
Une corde frappée est une corde que l’on excite en la déformant en
provoquant un choc bref sur une partie de cette corde à l’aide d’un
« marteau » comme cela est fait dans le piano (voir chapitre 9). A
l’instant 0, si on suppose un choc parfaitement élastique et très bref, la
forme de la corde n’a pas changé, par contre le point qui a subit le choc peut
être considéré comme ayant acquis une vitesse initiale V. La forme de la corde
ainsi que son champ de vitesse sont alors donnés par la figure 2-11 ci-dessous.
Figure
5-11
Champ des vitesses
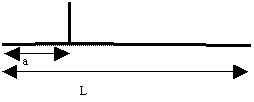
![]()
Champ des déformations

A l’instant t= 0, on a donc sur [0,L]:
|
|
(7)
V.3.2. Résolution de l’équation du mouvement
De la même façon qu’au paragraphe 1.2, on déduit immédiatement que tous
les Di sont nuls:
|
On a donc Dj = 0 quel que soit j. |
Si on multiplie par ![]() l’équation donnant Ci
et si on intègre de 0 à L, on obtient :
l’équation donnant Ci
et si on intègre de 0 à L, on obtient :
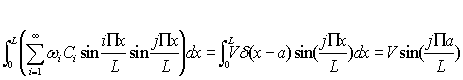
De laquelle on tire en applicquant la même méthode qu’au paragraphe
1-2:
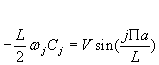
|
|
On en déduit deux propriétés immédiates :
- Cj , qui
est l’amplitude de l’harmonique j, décroît comme l’inverse de j; le son
résultant sera donc beaucoup plus riche que le son obtenu avec une corde
pincée.
- Cj s’annule pour ![]() , avec m=
0,1,2,3,...,n,...
, avec m=
0,1,2,3,...,n,...
On perd ainsi toutes les harmoniques qui auraient présenté un nœud en
a. Par exemple si on pince la corde en son milieu, on perd toutes les
harmoniques paires.
V.3.3. Visualisation
Pour visualiser le mouvement de la corde, nous allons prendre une corde
dont les caractéristiques sont les suivantes:
Longueur = L = 1 m
Tension = T = 100 N
Masse linéaire = r = ![]()
r est calculé en supposant que la corde est en acier, et a un diamétre
de 0,0002 m (deux dixième de millimétre); la masse volumique de l’acier est de
l’ordre de 8000 kg/m 3, la masse linéaire est alors de :
![]()
Avec ces données la vitesse de propagation de l’onde est de l’ordre de
630 m/s et la fréquence du son fondamental est de 315 Hertz, ce qui
correspondrait au Ré#3 . La période de la perturbation
est de 0,0032 secondes.
La forme de la corde à différents instants est donné sur les figures 5-12
et 5-13 ci-après. Pour tracer ces figures nous n’avons pris en compte que 13
harmoniques.
On constate bien que les perturbations se déplacent sur la corde à
vitesse constante et se réfléchissent aux extrémités.
Figure
5-12
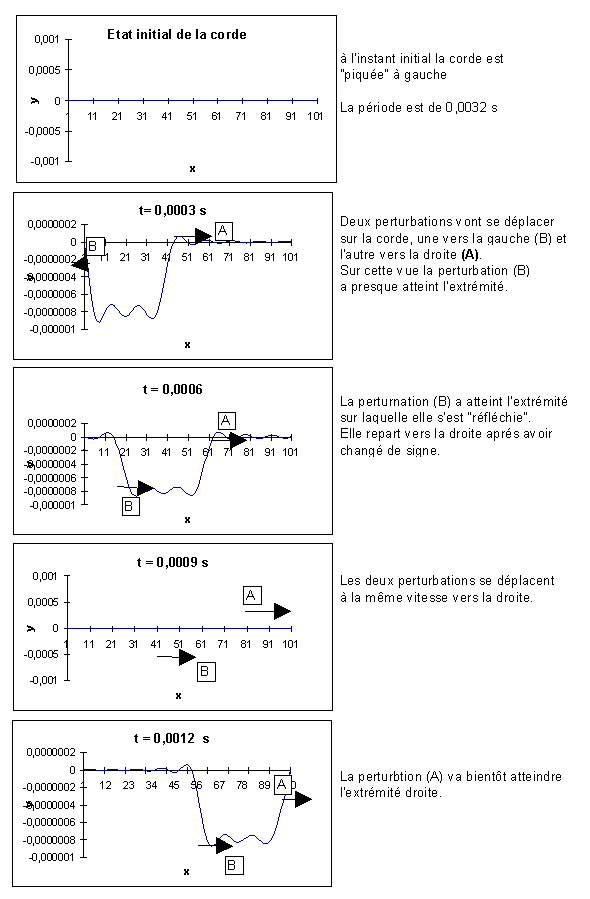
Figure 5-13
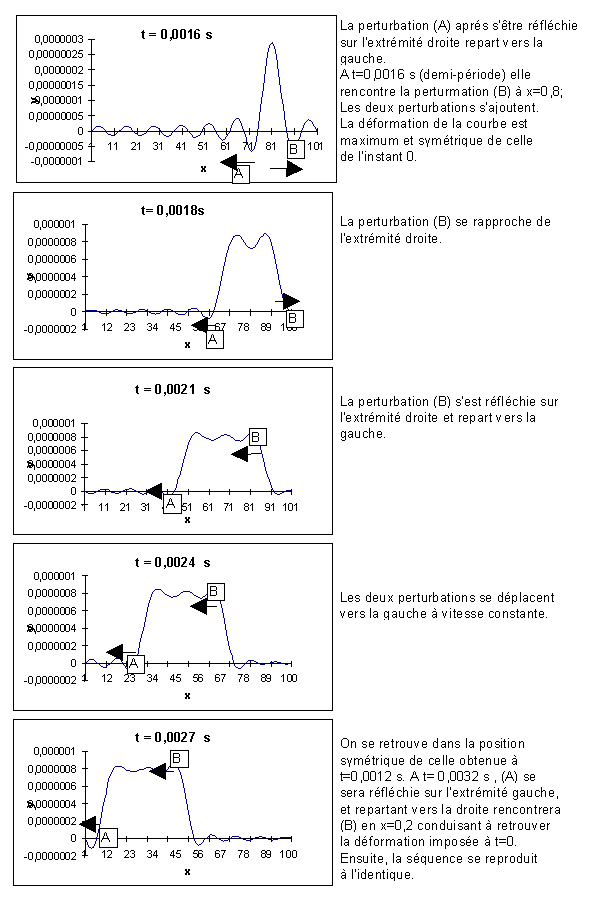
Figure 5-14