Le jeu

des segments

Ou irrégularités dans les distributions de séquence finie

Le jeu consiste à placer un nombre de pions maximum sur un segment sur lequel on définit des cases. Les pions sont placés en respectant les règles ci-après.

Une fois un pion placé, on ne peut plus le déplacer ensuite.

Si on veut placer le n° pion, on doit découper le segment en n parties égales : « cases ».

Si une de ces cases contient plus de 1 pion, on a perdu.

Si aucune case ne contient deux pions, une case et une seule est vide ; on peut alors placer le n° pion dans cette case.

On continue ainsi de pion en pion.

Exemple :

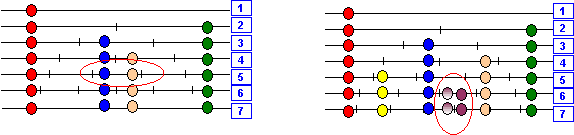
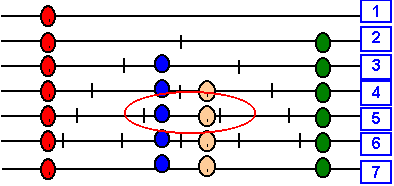
Deux cas sont illustrés ci-dessus :

1 : pour le premier cas on arrive à placer le 4° pion, mais au 5° rang on a deux pions dans le même segment ! On voit que l’on pourrait aller plus loin en déplaçant vers la gauche le 4° pion.

2 : pour le deuxième, on a déplacé vers la gauche le 4° pion ; on arrive à placer 6 pions, mais on voit que quelle que soit la position du 6° pion dans la case libre à ce niveau, on se retrouvera au 7° niveau avec deux pions dans une seule case (les deux positions du 6° pion sont indiquées par des nuances de violet).

I.2 Question

Trois questions découlent de la règle du jeu et de l’exemple précédent.

1 : Peut-on placer un nombre quelconque de pions ?

2 : Si, il y a une limite, quelle est-elle ?

3 : Pour le nombre maximum de pions possible, quelle est le nombre de solutions ?

I.3 La solution

Le problème peut être résolu par une approche mathématique et par une approche informatique. Nous allons étudier les deux.

II L’approche informatique

II.1 Définition d’une solution

Il faut, si l’on veut comptabiliser le nombre de solutions possibles pour un nombre N0 de pions définir une règle évitant de compter plusieurs fois la même solution. En effet, le segment étant continue, on voit évidemment que si on arrive à placer N0 pions, il y aura une infinité de solutions « géométriques ». Pour éviter cette situation on dira que deux solutions sont différentes si, pour le rang N0, elles conduisent à une séquence de placement des pions différents dans les N0 segments résultants. L’exemple ci-dessous illustre deux solutions identiques et deux différentes pour un rang 4.

Deux solutions identiques :

Deus solutions différentes :

Avec le symbolisme suivant :

De la même manière on constate que pour chaque solution, une solution symétrique existe :

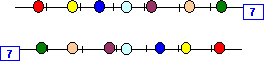
Solution de base

Solution symétrique

On se limitera donc dans la suite à ne compter que les solutions dont le premier pion est situé dans un intervalle ne dépassant pas le milieu du segment. Le double du nombre de solutions trouvé sera alors le nombre de solutions total. On remarque donc déjà que ce nombre sera toujours pair.

II.2 Quelques définitions

II.2.1 Un début d’algorithme pour des définitions

Si on reprend un des exemples conduisant à une impossibilité, tel le suivant :

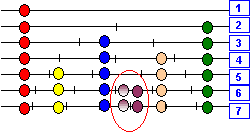
On constate que bien que le 6° pion puisse être placé au 6° rang, il conduit soit à avoir deux pions dans le 4° segment défini au rang 7, soit dans le 5° segment.

Nous appellerons « tranche » de rang n un segment de longueur 1/n.

Cela montre que quand on veut placer un pion au rang n et être sur qu’il ne va pas conduire, en prenant en compte les pions déjà placés (les n-1 autres pions), à une impossibilité à un rang N0 supérieur, il faut prendre en compte pour le choix de sa position, le placement des pions existant à tous les rangs compris entre n +1 et N. Pour cela, on déduit aisément qu’il faut considérer à ce rang n, tous les intervalles ayant comme bornes k/p, où p est un nombre entier compris entre n et N0, et k un nombre entier compris entre 1 et p. On constate immédiatement que le déplacement d’un pion d’un de ces intervalles à un autre conduira à deux solutions différentes ; on franchit en effet à un rang supérieur une tranche. Ces intervalles seront appelés des « cases ».

Compte tenue de la définition précédente, les cases sont définie pour un rang n donné et pour un nombre N0 maximum recherché donné.

Pour N0=7, il y a par exemple 18 cases calculées au rang 1 :

II.2.2 Quelques définitions utiles

Nous appellerons N0 le nombre objectif de pions à placer.

La situation dans laquelle on est quand on veut placer le p° pion, sera appelée situation de rang p.

Nous appellerons case i de rang p pour un objectif N0 le i° intervalle parmi les intervalles définis par les bornes k/n, où n est un nombre entier compris entre p et N0, et k un nombre entier compris entre 1 et n. En pratique on omettra de spécifier pour un objectif N0.

Le nombre de cases de rang 1 pour un objectif N0 est donné par le graphique suivant :

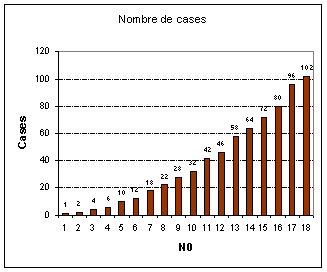
On appellera tranche de rang p, un des segments définis par [k/p ;(k+1)/p] avec 1 £ k £ (p-1). Ces tranches seront numérotées séquentiellement en partant de l’extrémité gauche du segment (0).

Une case i de rang p a pour borne deux entiers relatifs du type k/n et k’/n’ ; si la case correspond à [k/n, k’/n’]; on appellera numérateur et dénominateur de la case i de rang p les entiers k et n.

On appellera enfin limites inférieure, respectivement supérieure, de la tranche i de rang p, la première case de rang p appartenant à la tranche i, respectivement la dernière case de rang p appartenant à la tranche i.

II.3 Un algorithme pour trouver les solutions

L’algorithme que nous allons utiliser est, compte tenu des caractéristiques du problème telles qu’évoquées lors des définitions, relativement simple.

[1] Nous allons supposer que nous avons placé p-1 pions.

[2] Nous essayons de placer le p° pion.

Au rang p, les p-1 pions placés précédemment occupent p-1 tranches de rang p. Le p° pion doit donc être placé dans la tranche restante. Mais nous avons vu que de façon à ne compter que les solutions conduisant pour N0 à la même séquence de pions, il fallait définir la position du point p au rang p en tenant compte des cases de rang p. On va donc placer le pion p dans la première case de la tranche libre.

[3] Il nous faut ensuite être sur que ce pion ne conduira pas, pour les rangs supérieurs à avoir deux des p pions placés dans une même tranche. Pour cela nous allons vérifier que pour tous les points placés au rang p, quel que soit le rang supérieur inférieur à N0, il n’y a pas deux pions dans une même case.

[4] Si tel est le cas, on peut passer au rang supérieur (on va en [1] avec p=p+1).

[5] Si p est égal à N0, on une solution. On en cherche alors une autre en déplaçant le p° pion d’une case si cela est possible – on va alors en [2] – si ce n’est pas possible nous avons trouvé toutes les solutions.

[5] Si tel n’est pas le cas, et qu’il existe encore une case non essayée dans la tranche libre de rang p, on place le pion sur cette case et on teste de nouveau pour s’assurer que pour les rangs supérieurs il n’y aura pas deux pions dans une même tranche.( en fait on retourne en [3]).

[6] Si ce n’est pas possible, cela veut dire que la séquence obtenue au rang p-1 ne conduit à aucune solution. On doit donc modifier cette séquence. La séquence est modifié en plaçant le (p-1)° pion dans la case libre suivante de la tranche de rang (p-1). On passe donc alors à [3] avec p=p-1. Mais si p-1 est alors égal à 1, le jeu est terminé .

II.4 Structure du programme

La structure générale du programme est alors la suivante :

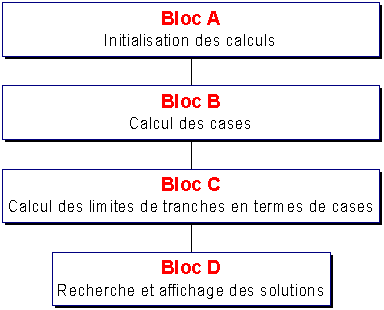
II.4.1 Définition des variables

Les numérateurs et dénominateurs de la case i de rang p seront dans les tableaux SN( i , p ) et SD( i, p). Le nombre maximum de cases sera stocké dans kmax1(p).

Les limites inférieure, respectivement supérieure, de la tranche i de rang p , seront dans les tableaux

Lboard (i , p) et Uboard ( i , p) respectivement.

Le tableaux TRKN ( j , n , p ) donneront le numéro k de la tranche de rang n à laquelle appartient la case j calculée au rang p.

Nous noterons nt( i ), la case de rang i dans laquelle est placé le i° pion.

Nous noterons ntk( k1 ), le rang i du pion qui conduit à occuper la tranche k1 au rang n.

II.4.2 Description du bloc A – Déclarations et initialisations

On trouvera dans le bloc A, les déclarations de variables et la mise à 0 des limites de cases pour le rang 2 :

SN ( 1,p), SN(2,p), SD(1,p) et SD(2,p).

II.4.3 Description du bloc B – Calcul des SN et SD

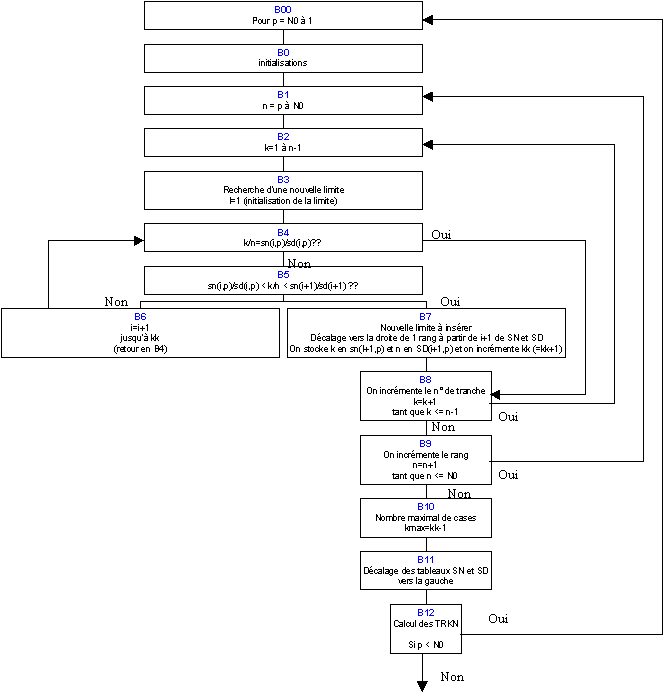
Voir le programme en C au paragraphe II.5.

II.4.4 Description du bloc C – Calcul des Uboard et Lboard

On définie ici les tableaux qui donnent les limites inférieures et supérieures d’une tranche kik de rang p, en termes de numéro de cases calculées au rang i : uboard ( kik, p, i) et lboard( kik , p , i) ; les cases appartenant à la tranche considérée. Cela permet si on a une tranche libre au rang p, de savoir pour tous les rangs inférieurs les cases dans lesquelles on peut mettre un pion qui se retrouve au rang p dans cette tranche.

Le bloc C est donc écrit suivant l’algorithme suivant :

Pour p étant égal à 1 jusqu'à N0

Pour kik valant 1 jusqu’à p, par pas de 1

Pour i valant 1 jusqu’à p par pas de 1

Initialisation de uboard (kik,p,i) à 0

Initialisation de lboard (kik,p,i) à 1

Pour i0 valant 1 jusqu’au nombre maximum de cases au rang i

Si kik/p = sn(i0,i)/sd(i0,i) alors uboard(kik,p,i) = i0

Si (kik-1)/p = sn(i0,i)/sd(i0,i) alors lboard(kik,p,i) = i0+1

Fin de la boucle sur i0

Fin de la boucle sur i

Fin de la boucle sur kik

Fin de la boucle sur p

II.4.5 Description du bloc D – Recherche des solutions

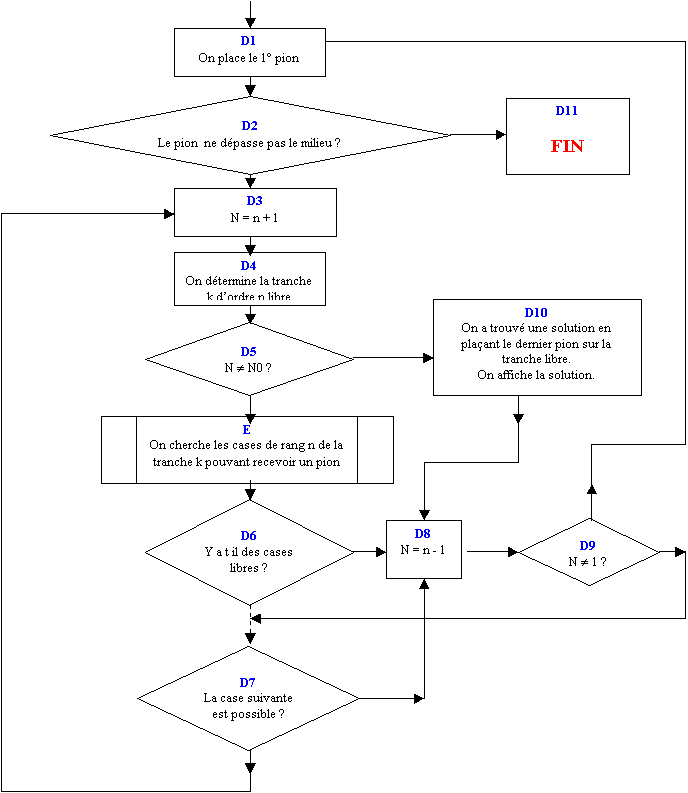
II.4.6 Description du bloc E – Identification des cases libres d’une tranche

Le but de cette recherche est de limiter lors des différentes itérations le nombre de cases d’une tranche à tester. En effet, quand on place un pion sur une tranche k libre à un rang n donné, les tranches situées de part et d’autres de cette tranche sont occupées par un pion mis à un rang inférieur : im1 pour la tranche située à gauche de la tranche k, ip1 pour celle située à droite. Chacun de ces pions occupant respectivement l a case jm1 calculée au rang im1, et jp1 calculée au rang ip1.

Cette fonction va donc éliminer les cases j calculées au rang n qui conduisent le pion i à partager une tranche à un rang supérieur à n avec le pion im1 ou le pion ip1.

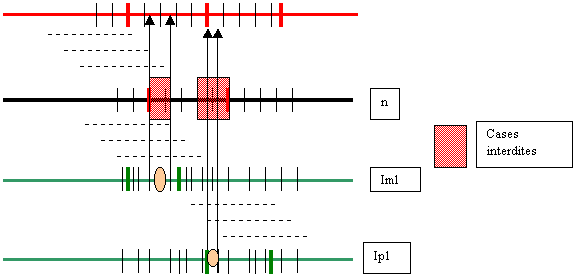
Voir la partie du programme repérée par E pour la traduction en C.

II.5 Le programme en C

#include <iostream.h>

// PROGRAMME DE DETERMINATION DES SOLUTIONS

// DU JEU DES SEGMENTS

// (ou irrégularités dans les distributions de séquences finies)

void main()

{

int i;

int sn[105][18];

int sd[105][18];

int kmax1[18];

int n0;

int kk;

int nm1;

int n;

int p;

int k;

int npe1;

int npe2;

int npm1;

int npm2;

int kmax;

int j;

int ii;

int trkn[105][18][18];

int ad;

int an;

int t1;

int t2;

int kik;

int uboard[19][19][19];

int lboard[19][19][19];

int sol;

int nt[18];

int ipos[18];

int ntk[18];

int nk[18];

int jj;

int k1;

int im1;

int ip1;

int jm1;

int jp1;

int np1;

int lb;

int ub;

int ctest;

int kn;

int k2;

int khk;

int ipsol;

int nn;

int imax[18];

int io;

int nn0;

cout <<" entrez le nombre maximal voulu pour le jeu: \n";

cin >> nn0;

for(n0=3;n0<=nn0;n0++)

{

cout << "\f recherche des solutions pour n= " << n0 << "\n";

// initialisation des tableaux;

for (p=n0;p>=1;p--)

{

// initialisation des tableaux sn et sd // B0

sn[1][p]=0; // B0

sd[1][p]=1; // B0

sn[2][p]=1; // B0

sd[2][p]=1; // B0

kk=2; // B0

// calcul des tableaux SN et SD // B1

for (n=p;n<=n0;n++) // boucle sur ETIQ51 // B1

{ // B1

if(n==1) goto ETIQ51; // B1

nm1=n-1; // B2

for (k=1;k<=nm1;k++) // boucle sur ETIQ41 // B2

{ // B2

i=0; // B2

ETIQ20: // B3

i=i+1; // B3

if(i>kk) goto ETIQ21; // B4

npe1=sn[i][p]*n; // B4

npm1=sd[i][p]*k; // B4

npe2=sn[i+1][p]*n; // B4

npm2=sd[i+1][p]*k; // B4

if (npe1==npm1) goto ETIQ41; // B4

if (npe1<npm1 && npm2<npe2) goto ETIQ21; // B5

goto ETIQ20; // B5

ETIQ21: // B7

ii=i+2; // B7

kk=kk+1; // B7

for (j=kk;j>=ii;j--) // B7

{ // B7

sn[j][p]=sn[j-1][p]; // B7

sd[j][p]=sd[j-1][p]; // B7

} // B7

sn[i+1][p]=k; // B7

sd[i+1][p]=n; // B7

ETIQ41:

i=i; // simplement pour faire une ligne sans action

}

ETIQ51:

i=i; // simplement pour faire une ligne sans action

}

kmax=kk-1; // B10

kmax1[p]=kmax; // B10

for(i=1;i<=kmax;i++) // B11

{ // B11

sn[i][p]=sn[i+1][p]; // B11

sd[i][p]=sd[i+1][p]; // B11

} // B11

// calcul des TRKN

for(n=1;n<=n0;n++) // B12

{ // B12

for(j=1;j<=kmax;j++) // B12

{ // B12

for(k=1;k<=n;k++) // B12

{ // B12

ad=sd[j][p]; // B12

an=sn[j][p]; // B12

t1=(k-1)*ad; // B12

t2=n*an; // B12

if(t1<t2) // B12

{ // B12

trkn[j][n][p]=k; // B12

} // B12

cout << "\nle nombre de cases est : "<< kmax1[1] << " \n ";

// calcul des Uboard et Lboard // C

for (p=1;p<=n0;p++) // C

{ // C

for(kik=1;kik<=p;kik++) // C

{ // C

for(i=1;i<=p;i++) // C

{ // C

uboard[kik][p][i]=0; // C

lboard[kik][p][i]=1; // C

for(io=1;io<=kmax1[i];io++) // C

{ // C

if (p*sn[io][i]==kik*sd[io][i]) uboard[kik][p][i]=io; // C

if (p*sn[io][i]==(kik-1)*sd[io][i]) lboard[kik][p][i]=io+1; // C

} // C

for(j=1;j<=kmax;j++)

{

sd[j][2]=sn[j][1];

}

// Recherche des solutions

// (1) on place le 1° pion ou on essaye la case supérieure // D1

ipsol=1; // D1

sol=0; // D1

n=0; // D1

nt[1]=1; // D1

ETIQ2: // D1

nt[1]=nt[1]+1; // D1

j=nt[1]; // D1

// (2) dépasse t-on le milieu?

if(2*sd[j][2]>sd[j][1]) goto ETIQ8; // D2

// (3) on passe à N= N+1

ETIQ3: // D3

n=n+1; // D3

// (4) - recherche de la tranche K libre

k=(n*(n+1))/2; // D4

// somme des numéro de tranche de 1 à n

nm1=n-1; // D4

for(i=1;i<=nm1;i++) // D4

{ // D4

jj=nt[i]; // D4

k1=trkn[jj][n][i]; // D4

ntk[k1]=i; // D4

k=k-k1; // D4

// on enlève le n° de tranche à la somme,

// le reste est la tranche vide

} // D4

// (5) n est-il égal à n0?

// si oui, on va afficher une solution

if(n==n0) goto ETIQ55; // D5

// (E) initialisation pour la recherche des cases possibles (ctest)

j=0; // E

if(k==1||k==n) goto ETIQ95; // E

im1=ntk[k-1]; // E

ip1=ntk[k+1]; // E

jm1=nt[im1]; // E

jp1=nt[ip1]; // E

ETIQ75: // E

np1=n+1; // E

lb=lboard[k][n][n]; // E

ub=uboard[k][n][n]; // E

ETIQ85: // E

for(ctest=lb;ctest<=ub;ctest++) // E

{ // E

for(nn=np1;nn<=n0;nn++) // E

{ // E

if(nn%n!=0) // E

{ // E

kn=trkn[ctest][nn][n]; // E

if(trkn[jm1][nn][im1]==kn) goto ETIQ906; // E

if(trkn[jp1][nn][ip1]==kn) goto ETIQ905; // E

} // E

j=j+1; // E

sn[j][n]=ctest; // E

// on stocke ctest dans sn pour économiser la mémoire

} // E

ETIQ905: // E

imax[n]=j; // E

if(j==0) goto ETIQ6; // E

ipos[n]=0; // E

goto ETIQ7; // E

ETIQ95: // E

if(k==1) k2=k+1; // E

if (k==n) k2=k-1; // E

im1=ntk[k2]; // E

ip1=im1; // E

jm1=nt[im1]; // E

jp1=jm1; // E

goto ETIQ75; // E

ETIQ906: // E

khk=trkn[jm1][nn][im1]; // E

lb=uboard[khk][nn][n]+1; // E

if(lb>ub) goto ETIQ905; // E

goto ETIQ85; // E

// (10) affichage d'une solution

ETIQ55: // D10

nt[n0]=k; // D10

sol=sol+1; // D10

for(ii=1;ii<=n0;ii++) // D10

{ // D10

jj=nt[ii]; // D10

nk[ii]=trkn[jj][n0][ii]; // D10

} // D10

if(ipsol!=nk[1]) // D10

// on saute une ligne quand le numéro du permier change

{ // D10

cout << "\n"; // D10

ipsol=nk[1]; // D10

} // D10

for(p=1;p<=n0;p++) // D10

{ // D10

cout << "\t" << nk[p]; // D10

} // D10

cout << "\n"; // D10

goto ETIQ6; // D10

// fin du programme

ETIQ8: // D11

cout << "\n Pour N= " << n0 << " le nombre de solution est " << sol; // D11

goto ETIQEND; // D11

// (8) on passe à n-1

ETIQ6: // D8

n=n-1; // D8

// (9) n est-il égal à 1

// si oui, on va alors vers un nouvel essai pour le premier point

if(n==1) goto ETIQ2; // D9

// (7) on place le pion n si possible

ETIQ7: // D7

ipos[n]=ipos[n]+1; // D7

i=ipos[n]; // D7

if(i>imax[n]) goto ETIQ6; // D7

nt[n]=sn[i][n]; // D7

goto ETIQ3; // on passe à n+1 // D7

ETIQEND: // D11

cout << " \n--------------- FIN --------------"; // D11

}

II.6 Les résultats

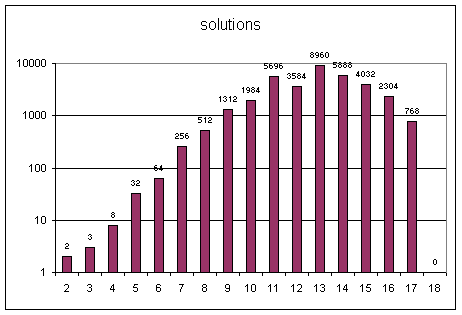
On a rajouté dans le programme une boucle pour chercher les solutions de 2 à un entier n maximum donné en entrée. Les résultats ci-dessous ont été obtenus pour n=2 à n=18. Le résultat ci-dessous est une copie du fichier résultat du programme précédent dans lequel, l’impression des solutions détaillées n’a pas été faite.

entrez le nombre maximal voulu pour le jeu:

recherche des solutions pour n= 3

Pour N= 3 le nombre de solution est 3

recherche des solutions pour n= 4

Pour N= 4 le nombre de solution est 8

recherche des solutions pour n= 5

Pour N= 5 le nombre de solution est 32

recherche des solutions pour n= 6

Pour N= 6 le nombre de solution est 64

recherche des solutions pour n= 7

Pour N= 7 le nombre de solution est 256

recherche des solutions pour n= 8

Pour N= 8 le nombre de solution est 512

recherche des solutions pour n= 9

Pour N= 9 le nombre de solution est 1312

recherche des solutions pour n= 10

Pour N= 10 le nombre de solution est 1984

recherche des solutions pour n= 11

Pour N= 11 le nombre de solution est 5696

recherche des solutions pour n= 12

Pour N= 12 le nombre de solution est 3584

recherche des solutions pour n= 13

Pour N= 13 le nombre de solution est 8960

recherche des solutions pour n= 14

Pour N= 14 le nombre de solution est 5888

recherche des solutions pour n= 15

Pour N= 15 le nombre de solution est 4032

recherche des solutions pour n= 16

Pour N= 16 le nombre de solution est 2304

recherche des solutions pour n= 17

Pour N= 17 le nombre de solution est 768

recherche des solutions pour n= 18

Pour N= 18 le nombre de solution est 0

Il y a donc un nombre limite qui est 17.

Pour 17 il y a 768 solutions

II.7 Historique

Le problème m’a été posé fin 1983 ; après quelques essais théoriques, j’ai décidé de rechercher la solution par le biais d’un programme informatique. Pour bâtir l’algorithme, on a commencé par chercher une solution à la main, ce qui nous a conduit à introduire la notion de tranches et de cases :

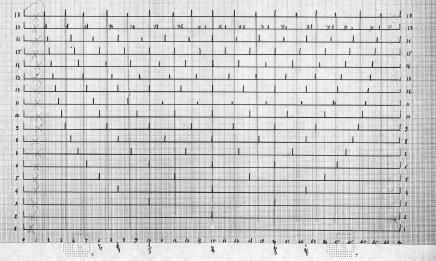
Le premier programme a tourné sur le SOLAR de l’école polytechnique ; le programme avait été mis sur « cartes perforées »….

Il n’a pas été possible d’obtenir alors des solutions pour N0=17 , le temps de calcul était trop long.

Le programme a ensuite été passé sur un UNIVAC de l’ENSTA. Cette fois l’ensemble des solutions pour n0=2 à 16 a été obtenu. Pour N0=17, le programme après avoir tourné 27 heures a trouvé 456 solutions ; il n’a pas été possible de le relancer !

Il ensuite été tourné sur un CRAY YMP; après 2h et 40 mn il a trouvé 480 solutions ! On a arrêté là.

Enfin, sur le COMPAQ presario personnel avec un pentium 2 à 266 Mhertz, toutes les solutions pour N0=17 ont été trouvé en 1 heure (à peu près) ! ! ! !

III L’approche théorique

Deux articles présentent les aspects théoriques du problème :

Irregularities in the distributions of finite sequences :

et A supplementary note on the irregularities of distributions :

IV Les solutions pour N0 = 17

Ci-dessous les sorties du programme pour N0=17 :

Recherche des solutions pour N=17

Le nombre de cases est : 96

Il y a 768 solutions qui sont les suivantes :

1 10 15 5 13 8 16 3 11 6 14 4 9 17 2 12 7

1 10 15 5 13 8 16 3 11 7 14 4 9 17 2 12 6

1 10 15 5 13 8 16 3 11 6 14 2 9 17 4 12 7

1 10 15 5 13 8 16 3 11 7 14 2 9 17 4 12 6

1 10 15 5 13 8 17 3 11 6 14 4 9 16 2 12 7

1 10 15 5 13 8 17 3 11 7 14 4 9 16 2 12 6

1 10 15 5 13 8 17 3 11 6 14 2 9 16 4 12 7

1 10 15 5 13 8 17 3 11 7 14 2 9 16 4 12 6

1 10 16 5 13 8 15 3 11 6 14 4 9 17 2 12 7

1 10 16 5 13 8 15 3 11 7 14 4 9 17 2 12 6

1 10 16 5 13 8 15 3 11 6 14 2 9 17 4 12 7

1 10 16 5 13 8 15 3 11 7 14 2 9 17 4 12 6

1 10 17 5 13 8 15 3 11 6 14 4 9 16 2 12 7

1 10 17 5 13 8 15 3 11 7 14 4 9 16 2 12 6

1 10 17 5 13 8 15 3 11 6 14 2 9 16 4 12 7

1 10 17 5 13 8 15 3 11 7 14 2 9 16 4 12 6

1 10 15 5 13 8 3 16 7 11 4 14 9 2 17 6 12

1 10 15 5 13 8 3 16 7 12 4 14 9 2 17 6 11

1 10 15 5 13 8 3 17 7 11 4 14 9 2 16 6 12

1 10 15 5 13 8 3 17 7 12 4 14 9 2 16 6 11

1 10 16 5 13 8 3 15 7 11 4 17 9 2 14 6 12

1 10 16 5 13 8 3 15 7 12 4 17 9 2 14 6 11

1 10 16 5 13 8 3 15 7 11 4 14 9 2 17 6 12

1 10 16 5 13 8 3 15 7 12 4 14 9 2 17 6 11

1 10 17 5 13 8 3 15 7 11 4 16 9 2 14 6 12

1 10 17 5 13 8 3 15 7 12 4 16 9 2 14 6 11

1 10 17 5 13 8 3 15 7 11 4 14 9 2 16 6 12

1 10 17 5 13 8 3 15 7 12 4 14 9 2 16 6 11

1 13 8 15 5 10 16 3 11 6 14 4 9 17 2 12 7

1 13 8 15 5 10 16 3 11 7 14 4 9 17 2 12 6

1 13 8 15 5 10 16 3 11 6 14 2 9 17 4 12 7

1 13 8 15 5 10 16 3 11 7 14 2 9 17 4 12 6

1 13 8 15 5 10 17 3 11 6 14 4 9 16 2 12 7

1 13 8 15 5 10 17 3 11 7 14 4 9 16 2 12 6

1 13 8 15 5 10 17 3 11 6 14 2 9 16 4 12 7

1 13 8 15 5 10 17 3 11 7 14 2 9 16 4 12 6

1 13 8 16 5 10 15 3 11 6 14 4 9 17 2 12 7

1 13 8 16 5 10 15 3 11 7 14 4 9 17 2 12 6

1 13 8 16 5 10 15 3 11 6 14 2 9 17 4 12 7

1 13 8 16 5 10 15 3 11 7 14 2 9 17 4 12 6

1 13 8 17 5 10 15 3 11 6 14 4 9 16 2 12 7

1 13 8 17 5 10 15 3 11 7 14 4 9 16 2 12 6

1 13 8 17 5 10 15 3 11 6 14 2 9 16 4 12 7

1 13 8 17 5 10 15 3 11 7 14 2 9 16 4 12 6

1 13 8 15 5 10 3 16 7 11 4 14 9 2 17 6 12

1 13 8 15 5 10 3 16 7 12 4 14 9 2 17 6 11

1 13 8 15 5 10 3 17 7 11 4 14 9 2 16 6 12

1 13 8 15 5 10 3 17 7 12 4 14 9 2 16 6 11

1 13 8 16 5 10 3 15 7 11 4 17 9 2 14 6 12

1 13 8 16 5 10 3 15 7 12 4 17 9 2 14 6 11

1 13 8 16 5 10 3 15 7 11 4 14 9 2 17 6 12

1 13 8 16 5 10 3 15 7 12 4 14 9 2 17 6 11

1 13 8 17 5 10 3 15 7 11 4 16 9 2 14 6 12

1 13 8 17 5 10 3 15 7 12 4 16 9 2 14 6 11

1 13 8 17 5 10 3 15 7 11 4 14 9 2 16 6 12

1 13 8 17 5 10 3 15 7 12 4 14 9 2 16 6 11

1 15 8 13 5 10 16 3 11 6 14 4 9 17 2 12 7

1 15 8 13 5 10 16 3 11 7 14 4 9 17 2 12 6

1 15 8 13 5 10 16 3 11 6 14 2 9 17 4 12 7

1 15 8 13 5 10 16 3 11 7 14 2 9 17 4 12 6

1 15 8 13 5 10 17 3 11 6 14 4 9 16 2 12 7

1 15 8 13 5 10 17 3 11 7 14 4 9 16 2 12 6

1 15 8 13 5 10 17 3 11 6 14 2 9 16 4 12 7

1 15 8 13 5 10 17 3 11 7 14 2 9 16 4 12 6

1 15 10 5 13 8 16 3 11 6 14 4 9 17 2 12 7

1 15 10 5 13 8 16 3 11 7 14 4 9 17 2 12 6

1 15 10 5 13 8 16 3 11 6 14 2 9 17 4 12 7

1 15 10 5 13 8 16 3 11 7 14 2 9 17 4 12 6

1 15 10 5 13 8 17 3 11 6 14 4 9 16 2 12 7

1 15 10 5 13 8 17 3 11 7 14 4 9 16 2 12 6

1 15 10 5 13 8 17 3 11 6 14 2 9 16 4 12 7

1 15 10 5 13 8 17 3 11 7 14 2 9 16 4 12 6

1 15 8 13 5 10 3 16 7 11 4 14 9 2 17 6 12

1 15 8 13 5 10 3 16 7 12 4 14 9 2 17 6 11

1 15 8 13 5 10 3 17 7 11 4 14 9 2 16 6 12

1 15 8 13 5 10 3 17 7 12 4 14 9 2 16 6 11

1 15 10 5 13 8 3 16 7 11 4 14 9 2 17 6 12

1 15 10 5 13 8 3 16 7 12 4 14 9 2 17 6 11

1 15 10 5 13 8 3 17 7 11 4 14 9 2 16 6 12

1 15 10 5 13 8 3 17 7 12 4 14 9 2 16 6 11

1 16 8 13 5 10 3 15 7 11 4 17 9 2 14 6 12

1 16 8 13 5 10 3 15 7 12 4 17 9 2 14 6 11

1 16 10 5 13 8 3 15 7 11 4 17 9 2 14 6 12

1 16 10 5 13 8 3 15 7 12 4 17 9 2 14 6 11

1 16 8 13 5 10 15 3 11 6 14 4 9 17 2 12 7

1 16 8 13 5 10 15 3 11 7 14 4 9 17 2 12 6

1 16 8 13 5 10 15 3 11 6 14 2 9 17 4 12 7

1 16 8 13 5 10 15 3 11 7 14 2 9 17 4 12 6

1 16 10 5 13 8 15 3 11 6 14 4 9 17 2 12 7

1 16 10 5 13 8 15 3 11 7 14 4 9 17 2 12 6

1 16 10 5 13 8 15 3 11 6 14 2 9 17 4 12 7

1 16 10 5 13 8 15 3 11 7 14 2 9 17 4 12 6

1 16 8 13 5 10 3 15 7 11 4 14 9 2 17 6 12

1 16 8 13 5 10 3 15 7 12 4 14 9 2 17 6 11

1 16 10 5 13 8 3 15 7 11 4 14 9 2 17 6 12

1 16 10 5 13 8 3 15 7 12 4 14 9 2 17 6 11

1 17 8 13 5 10 15 3 11 6 14 4 9 16 2 12 7

1 17 8 13 5 10 15 3 11 7 14 4 9 16 2 12 6

1 17 8 13 5 10 15 3 11 6 14 2 9 16 4 12 7

1 17 8 13 5 10 15 3 11 7 14 2 9 16 4 12 6

1 17 8 13 5 10 3 15 7 11 4 16 9 2 14 6 12

1 17 8 13 5 10 3 15 7 12 4 16 9 2 14 6 11

1 17 8 13 5 10 3 15 7 11 4 14 9 2 16 6 12

1 17 8 13 5 10 3 15 7 12 4 14 9 2 16 6 11

1 17 10 5 13 8 15 3 11 6 14 4 9 16 2 12 7

1 17 10 5 13 8 15 3 11 7 14 4 9 16 2 12 6

1 17 10 5 13 8 15 3 11 6 14 2 9 16 4 12 7

1 17 10 5 13 8 15 3 11 7 14 2 9 16 4 12 6

1 17 10 5 13 8 3 15 7 11 4 16 9 2 14 6 12

1 17 10 5 13 8 3 15 7 12 4 16 9 2 14 6 11

1 17 10 5 13 8 3 15 7 11 4 14 9 2 16 6 12

1 17 10 5 13 8 3 15 7 12 4 14 9 2 16 6 11

2 10 15 5 13 8 16 3 11 6 14 4 9 17 1 12 7

2 10 15 5 13 8 16 3 11 7 14 4 9 17 1 12 6

2 10 15 5 13 8 17 3 11 6 14 4 9 16 1 12 7

2 10 15 5 13 8 17 3 11 7 14 4 9 16 1 12 6

2 10 16 5 13 8 15 3 11 6 14 4 9 17 1 12 7

2 10 16 5 13 8 15 3 11 7 14 4 9 17 1 12 6

2 10 17 5 13 8 15 3 11 6 14 4 9 16 1 12 7

2 10 17 5 13 8 15 3 11 7 14 4 9 16 1 12 6

2 13 8 15 5 10 16 3 11 6 14 4 9 17 1 12 7

2 13 8 15 5 10 16 3 11 7 14 4 9 17 1 12 6

2 13 8 15 5 10 17 3 11 6 14 4 9 16 1 12 7

2 13 8 15 5 10 17 3 11 7 14 4 9 16 1 12 6

2 13 8 16 5 10 15 3 11 6 14 4 9 17 1 12 7

2 13 8 16 5 10 15 3 11 7 14 4 9 17 1 12 6

2 13 8 17 5 10 15 3 11 6 14 4 9 16 1 12 7

2 13 8 17 5 10 15 3 11 7 14 4 9 16 1 12 6

2 15 8 13 5 10 16 3 11 6 14 4 9 17 1 12 7

2 15 8 13 5 10 16 3 11 7 14 4 9 17 1 12 6

2 15 8 13 5 10 17 3 11 6 14 4 9 16 1 12 7

2 15 8 13 5 10 17 3 11 7 14 4 9 16 1 12 6

2 15 10 5 13 8 16 3 11 6 14 4 9 17 1 12 7

2 15 10 5 13 8 16 3 11 7 14 4 9 17 1 12 6

2 15 10 5 13 8 17 3 11 6 14 4 9 16 1 12 7

2 15 10 5 13 8 17 3 11 7 14 4 9 16 1 12 6

2 16 8 13 5 10 15 3 11 6 14 4 9 17 1 12 7

2 16 8 13 5 10 15 3 11 7 14 4 9 17 1 12 6

2 16 10 5 13 8 15 3 11 6 14 4 9 17 1 12 7

2 16 10 5 13 8 15 3 11 7 14 4 9 17 1 12 6

2 17 8 13 5 10 15 3 11 6 14 4 9 16 1 12 7

2 17 8 13 5 10 15 3 11 7 14 4 9 16 1 12 6

2 17 10 5 13 8 15 3 11 6 14 4 9 16 1 12 7

2 17 10 5 13 8 15 3 11 7 14 4 9 16 1 12 6

2 10 15 5 13 8 3 16 7 11 4 14 9 1 17 6 12

2 10 15 5 13 8 3 16 7 12 4 14 9 1 17 6 11

2 10 15 5 13 8 3 17 7 11 4 14 9 1 16 6 12

2 10 15 5 13 8 3 17 7 12 4 14 9 1 16 6 11

2 10 16 5 13 8 3 15 7 11 4 17 9 1 14 6 12

2 10 16 5 13 8 3 15 7 12 4 17 9 1 14 6 11

2 10 16 5 13 8 3 15 7 11 4 14 9 1 17 6 12

2 10 16 5 13 8 3 15 7 12 4 14 9 1 17 6 11

2 10 17 5 13 8 3 15 7 11 4 16 9 1 14 6 12

2 10 17 5 13 8 3 15 7 12 4 16 9 1 14 6 11

2 10 17 5 13 8 3 15 7 11 4 14 9 1 16 6 12

2 10 17 5 13 8 3 15 7 12 4 14 9 1 16 6 11

2 13 8 15 5 10 3 16 7 11 4 14 9 1 17 6 12

2 13 8 15 5 10 3 16 7 12 4 14 9 1 17 6 11

2 13 8 15 5 10 3 17 7 11 4 14 9 1 16 6 12

2 13 8 15 5 10 3 17 7 12 4 14 9 1 16 6 11

2 13 8 16 5 10 3 15 7 11 4 17 9 1 14 6 12

2 13 8 16 5 10 3 15 7 12 4 17 9 1 14 6 11

2 13 8 16 5 10 3 15 7 11 4 14 9 1 17 6 12

2 13 8 16 5 10 3 15 7 12 4 14 9 1 17 6 11

2 13 8 17 5 10 3 15 7 11 4 16 9 1 14 6 12

2 13 8 17 5 10 3 15 7 12 4 16 9 1 14 6 11

2 13 8 17 5 10 3 15 7 11 4 14 9 1 16 6 12

2 13 8 17 5 10 3 15 7 12 4 14 9 1 16 6 11

2 15 8 13 5 10 3 16 7 11 4 14 9 1 17 6 12

2 15 8 13 5 10 3 16 7 12 4 14 9 1 17 6 11

2 15 8 13 5 10 3 17 7 11 4 14 9 1 16 6 12

2 15 8 13 5 10 3 17 7 12 4 14 9 1 16 6 11

2 15 10 5 13 8 3 16 7 11 4 14 9 1 17 6 12

2 15 10 5 13 8 3 16 7 12 4 14 9 1 17 6 11

2 15 10 5 13 8 3 17 7 11 4 14 9 1 16 6 12

2 15 10 5 13 8 3 17 7 12 4 14 9 1 16 6 11

2 16 8 13 5 10 3 15 7 11 4 17 9 1 14 6 12

2 16 8 13 5 10 3 15 7 12 4 17 9 1 14 6 11

2 16 10 5 13 8 3 15 7 11 4 17 9 1 14 6 12

2 16 10 5 13 8 3 15 7 12 4 17 9 1 14 6 11

2 16 8 13 5 10 3 15 7 11 4 14 9 1 17 6 12

2 16 8 13 5 10 3 15 7 12 4 14 9 1 17 6 11

2 16 10 5 13 8 3 15 7 11 4 14 9 1 17 6 12

2 16 10 5 13 8 3 15 7 12 4 14 9 1 17 6 11

2 17 8 13 5 10 3 15 7 11 4 16 9 1 14 6 12

2 17 8 13 5 10 3 15 7 12 4 16 9 1 14 6 11

2 17 8 13 5 10 3 15 7 11 4 14 9 1 16 6 12

2 17 8 13 5 10 3 15 7 12 4 14 9 1 16 6 11

2 17 10 5 13 8 3 15 7 11 4 16 9 1 14 6 12

2 17 10 5 13 8 3 15 7 12 4 16 9 1 14 6 11

2 17 10 5 13 8 3 15 7 11 4 14 9 1 16 6 12

2 17 10 5 13 8 3 15 7 12 4 14 9 1 16 6 11

2 10 15 5 13 8 16 3 11 6 14 1 9 17 4 12 7

2 10 15 5 13 8 16 3 11 7 14 1 9 17 4 12 6

2 10 15 5 13 8 17 3 11 6 14 1 9 16 4 12 7

2 10 15 5 13 8 17 3 11 7 14 1 9 16 4 12 6

2 10 16 5 13 8 15 3 11 6 14 1 9 17 4 12 7

2 10 16 5 13 8 15 3 11 7 14 1 9 17 4 12 6

2 10 17 5 13 8 15 3 11 6 14 1 9 16 4 12 7

2 10 17 5 13 8 15 3 11 7 14 1 9 16 4 12 6

2 13 8 15 5 10 16 3 11 6 14 1 9 17 4 12 7

2 13 8 15 5 10 16 3 11 7 14 1 9 17 4 12 6

2 13 8 15 5 10 17 3 11 6 14 1 9 16 4 12 7

2 13 8 15 5 10 17 3 11 7 14 1 9 16 4 12 6

2 13 8 16 5 10 15 3 11 6 14 1 9 17 4 12 7

2 13 8 16 5 10 15 3 11 7 14 1 9 17 4 12 6

2 13 8 17 5 10 15 3 11 6 14 1 9 16 4 12 7

2 13 8 17 5 10 15 3 11 7 14 1 9 16 4 12 6

2 15 8 13 5 10 16 3 11 6 14 1 9 17 4 12 7

2 15 8 13 5 10 16 3 11 7 14 1 9 17 4 12 6

2 15 8 13 5 10 17 3 11 6 14 1 9 16 4 12 7

2 15 8 13 5 10 17 3 11 7 14 1 9 16 4 12 6

2 15 10 5 13 8 16 3 11 6 14 1 9 17 4 12 7

2 15 10 5 13 8 16 3 11 7 14 1 9 17 4 12 6

2 15 10 5 13 8 17 3 11 6 14 1 9 16 4 12 7

2 15 10 5 13 8 17 3 11 7 14 1 9 16 4 12 6

2 16 8 13 5 10 15 3 11 6 14 1 9 17 4 12 7

2 16 8 13 5 10 15 3 11 7 14 1 9 17 4 12 6

2 16 10 5 13 8 15 3 11 6 14 1 9 17 4 12 7

2 16 10 5 13 8 15 3 11 7 14 1 9 17 4 12 6

2 17 8 13 5 10 15 3 11 6 14 1 9 16 4 12 7

2 17 8 13 5 10 15 3 11 7 14 1 9 16 4 12 6

2 17 10 5 13 8 15 3 11 6 14 1 9 16 4 12 7

2 17 10 5 13 8 15 3 11 7 14 1 9 16 4 12 6

3 10 15 5 13 8 16 1 11 6 14 4 9 17 2 12 7

3 10 15 5 13 8 16 1 11 7 14 4 9 17 2 12 6

3 10 15 5 13 8 16 2 11 6 14 4 9 17 1 12 7

3 10 15 5 13 8 16 2 11 7 14 4 9 17 1 12 6

3 10 15 5 13 8 17 1 11 6 14 4 9 16 2 12 7

3 10 15 5 13 8 17 1 11 7 14 4 9 16 2 12 6

3 10 15 5 13 8 17 2 11 6 14 4 9 16 1 12 7

3 10 15 5 13 8 17 2 11 7 14 4 9 16 1 12 6

3 10 16 5 13 8 15 1 11 6 14 4 9 17 2 12 7

3 10 16 5 13 8 15 1 11 7 14 4 9 17 2 12 6

3 10 16 5 13 8 15 2 11 6 14 4 9 17 1 12 7

3 10 16 5 13 8 15 2 11 7 14 4 9 17 1 12 6

3 10 17 5 13 8 15 1 11 6 14 4 9 16 2 12 7

3 10 17 5 13 8 15 1 11 7 14 4 9 16 2 12 6

3 10 17 5 13 8 15 2 11 6 14 4 9 16 1 12 7

3 10 17 5 13 8 15 2 11 7 14 4 9 16 1 12 6

3 13 8 15 5 10 16 1 11 6 14 4 9 17 2 12 7

3 13 8 15 5 10 16 1 11 7 14 4 9 17 2 12 6

3 13 8 15 5 10 16 2 11 6 14 4 9 17 1 12 7

3 13 8 15 5 10 16 2 11 7 14 4 9 17 1 12 6

3 13 8 15 5 10 17 1 11 6 14 4 9 16 2 12 7

3 13 8 15 5 10 17 1 11 7 14 4 9 16 2 12 6

3 13 8 15 5 10 17 2 11 6 14 4 9 16 1 12 7

3 13 8 15 5 10 17 2 11 7 14 4 9 16 1 12 6

3 13 8 16 5 10 15 1 11 6 14 4 9 17 2 12 7

3 13 8 16 5 10 15 1 11 7 14 4 9 17 2 12 6

3 13 8 16 5 10 15 2 11 6 14 4 9 17 1 12 7

3 13 8 16 5 10 15 2 11 7 14 4 9 17 1 12 6

3 13 8 17 5 10 15 1 11 6 14 4 9 16 2 12 7

3 13 8 17 5 10 15 1 11 7 14 4 9 16 2 12 6

3 13 8 17 5 10 15 2 11 6 14 4 9 16 1 12 7

3 13 8 17 5 10 15 2 11 7 14 4 9 16 1 12 6

3 15 8 13 5 10 16 1 11 6 14 4 9 17 2 12 7

3 15 8 13 5 10 16 1 11 7 14 4 9 17 2 12 6

3 15 8 13 5 10 16 2 11 6 14 4 9 17 1 12 7

3 15 8 13 5 10 16 2 11 7 14 4 9 17 1 12 6

3 15 8 13 5 10 17 1 11 6 14 4 9 16 2 12 7

3 15 8 13 5 10 17 1 11 7 14 4 9 16 2 12 6

3 15 8 13 5 10 17 2 11 6 14 4 9 16 1 12 7

3 15 8 13 5 10 17 2 11 7 14 4 9 16 1 12 6

3 15 10 5 13 8 16 1 11 6 14 4 9 17 2 12 7

3 15 10 5 13 8 16 1 11 7 14 4 9 17 2 12 6

3 15 10 5 13 8 16 2 11 6 14 4 9 17 1 12 7

3 15 10 5 13 8 16 2 11 7 14 4 9 17 1 12 6

3 15 10 5 13 8 17 1 11 6 14 4 9 16 2 12 7

3 15 10 5 13 8 17 1 11 7 14 4 9 16 2 12 6

3 15 10 5 13 8 17 2 11 6 14 4 9 16 1 12 7

3 15 10 5 13 8 17 2 11 7 14 4 9 16 1 12 6

3 16 8 13 5 10 15 1 11 6 14 4 9 17 2 12 7

3 16 8 13 5 10 15 1 11 7 14 4 9 17 2 12 6

3 16 8 13 5 10 15 2 11 6 14 4 9 17 1 12 7

3 16 8 13 5 10 15 2 11 7 14 4 9 17 1 12 6

3 16 10 5 13 8 15 1 11 6 14 4 9 17 2 12 7

3 16 10 5 13 8 15 1 11 7 14 4 9 17 2 12 6

3 16 10 5 13 8 15 2 11 6 14 4 9 17 1 12 7

3 16 10 5 13 8 15 2 11 7 14 4 9 17 1 12 6

3 17 8 13 5 10 15 1 11 6 14 4 9 16 2 12 7

3 17 8 13 5 10 15 1 11 7 14 4 9 16 2 12 6

3 17 8 13 5 10 15 2 11 6 14 4 9 16 1 12 7

3 17 8 13 5 10 15 2 11 7 14 4 9 16 1 12 6

3 17 10 5 13 8 15 1 11 6 14 4 9 16 2 12 7

3 17 10 5 13 8 15 1 11 7 14 4 9 16 2 12 6

3 17 10 5 13 8 15 2 11 6 14 4 9 16 1 12 7

3 17 10 5 13 8 15 2 11 7 14 4 9 16 1 12 6

3 10 15 5 13 8 1 16 7 11 4 14 9 2 17 6 12

3 10 15 5 13 8 1 16 7 12 4 14 9 2 17 6 11

3 10 15 5 13 8 1 17 7 11 4 14 9 2 16 6 12

3 10 15 5 13 8 1 17 7 12 4 14 9 2 16 6 11

3 10 15 5 13 8 2 16 7 11 4 14 9 1 17 6 12

3 10 15 5 13 8 2 16 7 12 4 14 9 1 17 6 11

3 10 15 5 13 8 2 17 7 11 4 14 9 1 16 6 12

3 10 15 5 13 8 2 17 7 12 4 14 9 1 16 6 11

3 10 16 5 13 8 1 15 7 11 4 17 9 2 14 6 12

3 10 16 5 13 8 1 15 7 12 4 17 9 2 14 6 11

3 10 16 5 13 8 2 15 7 11 4 17 9 1 14 6 12

3 10 16 5 13 8 2 15 7 12 4 17 9 1 14 6 11

3 10 16 5 13 8 1 15 7 11 4 14 9 2 17 6 12

3 10 16 5 13 8 1 15 7 12 4 14 9 2 17 6 11

3 10 16 5 13 8 2 15 7 11 4 14 9 1 17 6 12

3 10 16 5 13 8 2 15 7 12 4 14 9 1 17 6 11

3 10 17 5 13 8 1 15 7 11 4 16 9 2 14 6 12

3 10 17 5 13 8 1 15 7 12 4 16 9 2 14 6 11

3 10 17 5 13 8 1 15 7 11 4 14 9 2 16 6 12

3 10 17 5 13 8 1 15 7 12 4 14 9 2 16 6 11

3 10 17 5 13 8 2 15 7 11 4 16 9 1 14 6 12

3 10 17 5 13 8 2 15 7 12 4 16 9 1 14 6 11

3 10 17 5 13 8 2 15 7 11 4 14 9 1 16 6 12

3 10 17 5 13 8 2 15 7 12 4 14 9 1 16 6 11

3 13 8 15 5 10 1 16 7 11 4 14 9 2 17 6 12

3 13 8 15 5 10 1 16 7 12 4 14 9 2 17 6 11

3 13 8 15 5 10 1 17 7 11 4 14 9 2 16 6 12

3 13 8 15 5 10 1 17 7 12 4 14 9 2 16 6 11

3 13 8 15 5 10 2 16 7 11 4 14 9 1 17 6 12

3 13 8 15 5 10 2 16 7 12 4 14 9 1 17 6 11

3 13 8 15 5 10 2 17 7 11 4 14 9 1 16 6 12

3 13 8 15 5 10 2 17 7 12 4 14 9 1 16 6 11

3 13 8 16 5 10 1 15 7 11 4 17 9 2 14 6 12

3 13 8 16 5 10 1 15 7 12 4 17 9 2 14 6 11

3 13 8 16 5 10 2 15 7 11 4 17 9 1 14 6 12

3 13 8 16 5 10 2 15 7 12 4 17 9 1 14 6 11

3 13 8 16 5 10 1 15 7 11 4 14 9 2 17 6 12

3 13 8 16 5 10 1 15 7 12 4 14 9 2 17 6 11

3 13 8 16 5 10 2 15 7 11 4 14 9 1 17 6 12

3 13 8 16 5 10 2 15 7 12 4 14 9 1 17 6 11

3 13 8 17 5 10 1 15 7 11 4 16 9 2 14 6 12

3 13 8 17 5 10 1 15 7 12 4 16 9 2 14 6 11

3 13 8 17 5 10 1 15 7 11 4 14 9 2 16 6 12

3 13 8 17 5 10 1 15 7 12 4 14 9 2 16 6 11

3 13 8 17 5 10 2 15 7 11 4 16 9 1 14 6 12

3 13 8 17 5 10 2 15 7 12 4 16 9 1 14 6 11

3 13 8 17 5 10 2 15 7 11 4 14 9 1 16 6 12

3 13 8 17 5 10 2 15 7 12 4 14 9 1 16 6 11

3 15 8 13 5 10 1 16 7 11 4 14 9 2 17 6 12

3 15 8 13 5 10 1 16 7 12 4 14 9 2 17 6 11

3 15 8 13 5 10 1 17 7 11 4 14 9 2 16 6 12

3 15 8 13 5 10 1 17 7 12 4 14 9 2 16 6 11

3 15 8 13 5 10 2 16 7 11 4 14 9 1 17 6 12

3 15 8 13 5 10 2 16 7 12 4 14 9 1 17 6 11

3 15 8 13 5 10 2 17 7 11 4 14 9 1 16 6 12

3 15 8 13 5 10 2 17 7 12 4 14 9 1 16 6 11

3 15 10 5 13 8 1 16 7 11 4 14 9 2 17 6 12

3 15 10 5 13 8 1 16 7 12 4 14 9 2 17 6 11

3 15 10 5 13 8 1 17 7 11 4 14 9 2 16 6 12

3 15 10 5 13 8 1 17 7 12 4 14 9 2 16 6 11

3 15 10 5 13 8 2 16 7 11 4 14 9 1 17 6 12

3 15 10 5 13 8 2 16 7 12 4 14 9 1 17 6 11

3 15 10 5 13 8 2 17 7 11 4 14 9 1 16 6 12

3 15 10 5 13 8 2 17 7 12 4 14 9 1 16 6 11

3 16 8 13 5 10 1 15 7 11 4 17 9 2 14 6 12

3 16 8 13 5 10 1 15 7 12 4 17 9 2 14 6 11

3 16 8 13 5 10 2 15 7 11 4 17 9 1 14 6 12

3 16 8 13 5 10 2 15 7 12 4 17 9 1 14 6 11

3 16 10 5 13 8 1 15 7 11 4 17 9 2 14 6 12

3 16 10 5 13 8 1 15 7 12 4 17 9 2 14 6 11

3 16 10 5 13 8 2 15 7 11 4 17 9 1 14 6 12

3 16 10 5 13 8 2 15 7 12 4 17 9 1 14 6 11

3 16 8 13 5 10 1 15 7 11 4 14 9 2 17 6 12

3 16 8 13 5 10 1 15 7 12 4 14 9 2 17 6 11

3 16 8 13 5 10 2 15 7 11 4 14 9 1 17 6 12

3 16 8 13 5 10 2 15 7 12 4 14 9 1 17 6 11

3 16 10 5 13 8 1 15 7 11 4 14 9 2 17 6 12

3 16 10 5 13 8 1 15 7 12 4 14 9 2 17 6 11

3 16 10 5 13 8 2 15 7 11 4 14 9 1 17 6 12

3 16 10 5 13 8 2 15 7 12 4 14 9 1 17 6 11

3 17 8 13 5 10 1 15 7 11 4 16 9 2 14 6 12

3 17 8 13 5 10 1 15 7 12 4 16 9 2 14 6 11

3 17 8 13 5 10 1 15 7 11 4 14 9 2 16 6 12

3 17 8 13 5 10 1 15 7 12 4 14 9 2 16 6 11

3 17 8 13 5 10 2 15 7 11 4 16 9 1 14 6 12

3 17 8 13 5 10 2 15 7 12 4 16 9 1 14 6 11

3 17 8 13 5 10 2 15 7 11 4 14 9 1 16 6 12

3 17 8 13 5 10 2 15 7 12 4 14 9 1 16 6 11

3 17 10 5 13 8 1 15 7 11 4 16 9 2 14 6 12

3 17 10 5 13 8 1 15 7 12 4 16 9 2 14 6 11

3 17 10 5 13 8 1 15 7 11 4 14 9 2 16 6 12

3 17 10 5 13 8 1 15 7 12 4 14 9 2 16 6 11

3 17 10 5 13 8 2 15 7 11 4 16 9 1 14 6 12

3 17 10 5 13 8 2 15 7 12 4 16 9 1 14 6 11

3 17 10 5 13 8 2 15 7 11 4 14 9 1 16 6 12

3 17 10 5 13 8 2 15 7 12 4 14 9 1 16 6 11

5 10 15 1 13 8 16 3 11 6 14 4 9 17 2 12 7

5 10 15 1 13 8 16 3 11 7 14 4 9 17 2 12 6

5 10 15 1 13 8 16 3 11 6 14 2 9 17 4 12 7

5 10 15 1 13 8 16 3 11 7 14 2 9 17 4 12 6

5 10 15 1 13 8 17 3 11 6 14 4 9 16 2 12 7

5 10 15 1 13 8 17 3 11 7 14 4 9 16 2 12 6

5 10 15 1 13 8 17 3 11 6 14 2 9 16 4 12 7

5 10 15 1 13 8 17 3 11 7 14 2 9 16 4 12 6

5 10 15 2 13 8 16 3 11 6 14 4 9 17 1 12 7

5 10 15 2 13 8 16 3 11 7 14 4 9 17 1 12 6

5 10 15 2 13 8 17 3 11 6 14 4 9 16 1 12 7

5 10 15 2 13 8 17 3 11 7 14 4 9 16 1 12 6

5 10 15 2 13 8 16 3 11 6 14 1 9 17 4 12 7

5 10 15 2 13 8 16 3 11 7 14 1 9 17 4 12 6

5 10 15 2 13 8 17 3 11 6 14 1 9 16 4 12 7

5 10 15 2 13 8 17 3 11 7 14 1 9 16 4 12 6

5 10 15 3 13 8 16 1 11 6 14 4 9 17 2 12 7

5 10 15 3 13 8 16 1 11 7 14 4 9 17 2 12 6

5 10 15 3 13 8 16 2 11 6 14 4 9 17 1 12 7

5 10 15 3 13 8 16 2 11 7 14 4 9 17 1 12 6

5 10 15 3 13 8 17 1 11 6 14 4 9 16 2 12 7

5 10 15 3 13 8 17 1 11 7 14 4 9 16 2 12 6

5 10 15 3 13 8 17 2 11 6 14 4 9 16 1 12 7

5 10 15 3 13 8 17 2 11 7 14 4 9 16 1 12 6

5 10 16 1 13 8 15 3 11 6 14 4 9 17 2 12 7

5 10 16 1 13 8 15 3 11 7 14 4 9 17 2 12 6

5 10 16 1 13 8 15 3 11 6 14 2 9 17 4 12 7

5 10 16 1 13 8 15 3 11 7 14 2 9 17 4 12 6

5 10 16 2 13 8 15 3 11 6 14 4 9 17 1 12 7

5 10 16 2 13 8 15 3 11 7 14 4 9 17 1 12 6

5 10 16 2 13 8 15 3 11 6 14 1 9 17 4 12 7

5 10 16 2 13 8 15 3 11 7 14 1 9 17 4 12 6

5 10 16 3 13 8 15 1 11 6 14 4 9 17 2 12 7

5 10 16 3 13 8 15 1 11 7 14 4 9 17 2 12 6

5 10 16 3 13 8 15 2 11 6 14 4 9 17 1 12 7

5 10 16 3 13 8 15 2 11 7 14 4 9 17 1 12 6

5 10 17 1 13 8 15 3 11 6 14 4 9 16 2 12 7

5 10 17 1 13 8 15 3 11 7 14 4 9 16 2 12 6

5 10 17 1 13 8 15 3 11 6 14 2 9 16 4 12 7

5 10 17 1 13 8 15 3 11 7 14 2 9 16 4 12 6

5 10 17 2 13 8 15 3 11 6 14 4 9 16 1 12 7

5 10 17 2 13 8 15 3 11 7 14 4 9 16 1 12 6

5 10 17 2 13 8 15 3 11 6 14 1 9 16 4 12 7

5 10 17 2 13 8 15 3 11 7 14 1 9 16 4 12 6

5 10 17 3 13 8 15 1 11 6 14 4 9 16 2 12 7

5 10 17 3 13 8 15 1 11 7 14 4 9 16 2 12 6

5 10 17 3 13 8 15 2 11 6 14 4 9 16 1 12 7

5 10 17 3 13 8 15 2 11 7 14 4 9 16 1 12 6

5 15 10 1 13 8 16 3 11 6 14 4 9 17 2 12 7

5 15 10 1 13 8 16 3 11 7 14 4 9 17 2 12 6

5 15 10 1 13 8 16 3 11 6 14 2 9 17 4 12 7

5 15 10 1 13 8 16 3 11 7 14 2 9 17 4 12 6

5 15 10 1 13 8 17 3 11 6 14 4 9 16 2 12 7

5 15 10 1 13 8 17 3 11 7 14 4 9 16 2 12 6

5 15 10 1 13 8 17 3 11 6 14 2 9 16 4 12 7

5 15 10 1 13 8 17 3 11 7 14 2 9 16 4 12 6

5 15 10 2 13 8 16 3 11 6 14 4 9 17 1 12 7

5 15 10 2 13 8 16 3 11 7 14 4 9 17 1 12 6

5 15 10 2 13 8 17 3 11 6 14 4 9 16 1 12 7

5 15 10 2 13 8 17 3 11 7 14 4 9 16 1 12 6

5 15 10 2 13 8 16 3 11 6 14 1 9 17 4 12 7

5 15 10 2 13 8 16 3 11 7 14 1 9 17 4 12 6

5 15 10 2 13 8 17 3 11 6 14 1 9 16 4 12 7

5 15 10 2 13 8 17 3 11 7 14 1 9 16 4 12 6

5 15 10 3 13 8 16 1 11 6 14 4 9 17 2 12 7

5 15 10 3 13 8 16 1 11 7 14 4 9 17 2 12 6

5 15 10 3 13 8 16 2 11 6 14 4 9 17 1 12 7

5 15 10 3 13 8 16 2 11 7 14 4 9 17 1 12 6

5 15 10 3 13 8 17 1 11 6 14 4 9 16 2 12 7

5 15 10 3 13 8 17 1 11 7 14 4 9 16 2 12 6

5 15 10 3 13 8 17 2 11 6 14 4 9 16 1 12 7

5 15 10 3 13 8 17 2 11 7 14 4 9 16 1 12 6

5 16 10 1 13 8 15 3 11 6 14 4 9 17 2 12 7

5 16 10 1 13 8 15 3 11 7 14 4 9 17 2 12 6

5 16 10 1 13 8 15 3 11 6 14 2 9 17 4 12 7

5 16 10 1 13 8 15 3 11 7 14 2 9 17 4 12 6

5 16 10 2 13 8 15 3 11 6 14 4 9 17 1 12 7

5 16 10 2 13 8 15 3 11 7 14 4 9 17 1 12 6

5 16 10 2 13 8 15 3 11 6 14 1 9 17 4 12 7

5 16 10 2 13 8 15 3 11 7 14 1 9 17 4 12 6

5 16 10 3 13 8 15 1 11 6 14 4 9 17 2 12 7

5 16 10 3 13 8 15 1 11 7 14 4 9 17 2 12 6

5 16 10 3 13 8 15 2 11 6 14 4 9 17 1 12 7

5 16 10 3 13 8 15 2 11 7 14 4 9 17 1 12 6

5 17 10 1 13 8 15 3 11 6 14 4 9 16 2 12 7

5 17 10 1 13 8 15 3 11 7 14 4 9 16 2 12 6

5 17 10 1 13 8 15 3 11 6 14 2 9 16 4 12 7

5 17 10 1 13 8 15 3 11 7 14 2 9 16 4 12 6

5 17 10 2 13 8 15 3 11 6 14 4 9 16 1 12 7

5 17 10 2 13 8 15 3 11 7 14 4 9 16 1 12 6

5 17 10 2 13 8 15 3 11 6 14 1 9 16 4 12 7

5 17 10 2 13 8 15 3 11 7 14 1 9 16 4 12 6

5 17 10 3 13 8 15 1 11 6 14 4 9 16 2 12 7

5 17 10 3 13 8 15 1 11 7 14 4 9 16 2 12 6

5 17 10 3 13 8 15 2 11 6 14 4 9 16 1 12 7

5 17 10 3 13 8 15 2 11 7 14 4 9 16 1 12 6

5 10 15 1 13 8 3 16 7 11 4 14 9 2 17 6 12

5 10 15 1 13 8 3 16 7 12 4 14 9 2 17 6 11

5 10 15 1 13 8 3 17 7 11 4 14 9 2 16 6 12

5 10 15 1 13 8 3 17 7 12 4 14 9 2 16 6 11

5 10 15 2 13 8 3 16 7 11 4 14 9 1 17 6 12

5 10 15 2 13 8 3 16 7 12 4 14 9 1 17 6 11

5 10 15 2 13 8 3 17 7 11 4 14 9 1 16 6 12

5 10 15 2 13 8 3 17 7 12 4 14 9 1 16 6 11

5 10 15 3 13 8 1 16 7 11 4 14 9 2 17 6 12

5 10 15 3 13 8 1 16 7 12 4 14 9 2 17 6 11

5 10 15 3 13 8 1 17 7 11 4 14 9 2 16 6 12

5 10 15 3 13 8 1 17 7 12 4 14 9 2 16 6 11

5 10 15 3 13 8 2 16 7 11 4 14 9 1 17 6 12

5 10 15 3 13 8 2 16 7 12 4 14 9 1 17 6 11

5 10 15 3 13 8 2 17 7 11 4 14 9 1 16 6 12

5 10 15 3 13 8 2 17 7 12 4 14 9 1 16 6 11

5 10 16 1 13 8 3 15 7 11 4 17 9 2 14 6 12

5 10 16 1 13 8 3 15 7 12 4 17 9 2 14 6 11

5 10 16 2 13 8 3 15 7 11 4 17 9 1 14 6 12

5 10 16 2 13 8 3 15 7 12 4 17 9 1 14 6 11

5 10 16 3 13 8 1 15 7 11 4 17 9 2 14 6 12

5 10 16 3 13 8 1 15 7 12 4 17 9 2 14 6 11

5 10 16 3 13 8 2 15 7 11 4 17 9 1 14 6 12

5 10 16 3 13 8 2 15 7 12 4 17 9 1 14 6 11

5 10 16 1 13 8 3 15 7 11 4 14 9 2 17 6 12

5 10 16 1 13 8 3 15 7 12 4 14 9 2 17 6 11

5 10 16 2 13 8 3 15 7 11 4 14 9 1 17 6 12

5 10 16 2 13 8 3 15 7 12 4 14 9 1 17 6 11

5 10 16 3 13 8 1 15 7 11 4 14 9 2 17 6 12

5 10 16 3 13 8 1 15 7 12 4 14 9 2 17 6 11

5 10 16 3 13 8 2 15 7 11 4 14 9 1 17 6 12

5 10 16 3 13 8 2 15 7 12 4 14 9 1 17 6 11

5 10 17 1 13 8 3 15 7 11 4 16 9 2 14 6 12

5 10 17 1 13 8 3 15 7 12 4 16 9 2 14 6 11

5 10 17 1 13 8 3 15 7 11 4 14 9 2 16 6 12

5 10 17 1 13 8 3 15 7 12 4 14 9 2 16 6 11

5 10 17 2 13 8 3 15 7 11 4 16 9 1 14 6 12

5 10 17 2 13 8 3 15 7 12 4 16 9 1 14 6 11

5 10 17 2 13 8 3 15 7 11 4 14 9 1 16 6 12

5 10 17 2 13 8 3 15 7 12 4 14 9 1 16 6 11

5 10 17 3 13 8 1 15 7 11 4 16 9 2 14 6 12

5 10 17 3 13 8 1 15 7 12 4 16 9 2 14 6 11

5 10 17 3 13 8 1 15 7 11 4 14 9 2 16 6 12

5 10 17 3 13 8 1 15 7 12 4 14 9 2 16 6 11

5 10 17 3 13 8 2 15 7 11 4 16 9 1 14 6 12

5 10 17 3 13 8 2 15 7 12 4 16 9 1 14 6 11

5 10 17 3 13 8 2 15 7 11 4 14 9 1 16 6 12

5 10 17 3 13 8 2 15 7 12 4 14 9 1 16 6 11

5 15 10 1 13 8 3 16 7 11 4 14 9 2 17 6 12

5 15 10 1 13 8 3 16 7 12 4 14 9 2 17 6 11

5 15 10 1 13 8 3 17 7 11 4 14 9 2 16 6 12

5 15 10 1 13 8 3 17 7 12 4 14 9 2 16 6 11

5 15 10 2 13 8 3 16 7 11 4 14 9 1 17 6 12

5 15 10 2 13 8 3 16 7 12 4 14 9 1 17 6 11

5 15 10 2 13 8 3 17 7 11 4 14 9 1 16 6 12

5 15 10 2 13 8 3 17 7 12 4 14 9 1 16 6 11

5 15 10 3 13 8 1 16 7 11 4 14 9 2 17 6 12

5 15 10 3 13 8 1 16 7 12 4 14 9 2 17 6 11

5 15 10 3 13 8 1 17 7 11 4 14 9 2 16 6 12

5 15 10 3 13 8 1 17 7 12 4 14 9 2 16 6 11

5 15 10 3 13 8 2 16 7 11 4 14 9 1 17 6 12

5 15 10 3 13 8 2 16 7 12 4 14 9 1 17 6 11

5 15 10 3 13 8 2 17 7 11 4 14 9 1 16 6 12

5 15 10 3 13 8 2 17 7 12 4 14 9 1 16 6 11

5 16 10 1 13 8 3 15 7 11 4 17 9 2 14 6 12

5 16 10 1 13 8 3 15 7 12 4 17 9 2 14 6 11

5 16 10 2 13 8 3 15 7 11 4 17 9 1 14 6 12

5 16 10 2 13 8 3 15 7 12 4 17 9 1 14 6 11

5 16 10 3 13 8 1 15 7 11 4 17 9 2 14 6 12

5 16 10 3 13 8 1 15 7 12 4 17 9 2 14 6 11

5 16 10 3 13 8 2 15 7 11 4 17 9 1 14 6 12

5 16 10 3 13 8 2 15 7 12 4 17 9 1 14 6 11

5 16 10 1 13 8 3 15 7 11 4 14 9 2 17 6 12

5 16 10 1 13 8 3 15 7 12 4 14 9 2 17 6 11

5 16 10 2 13 8 3 15 7 11 4 14 9 1 17 6 12

5 16 10 2 13 8 3 15 7 12 4 14 9 1 17 6 11

5 16 10 3 13 8 1 15 7 11 4 14 9 2 17 6 12

5 16 10 3 13 8 1 15 7 12 4 14 9 2 17 6 11

5 16 10 3 13 8 2 15 7 11 4 14 9 1 17 6 12

5 16 10 3 13 8 2 15 7 12 4 14 9 1 17 6 11

5 17 10 1 13 8 3 15 7 11 4 16 9 2 14 6 12

5 17 10 1 13 8 3 15 7 12 4 16 9 2 14 6 11

5 17 10 1 13 8 3 15 7 11 4 14 9 2 16 6 12

5 17 10 1 13 8 3 15 7 12 4 14 9 2 16 6 11

5 17 10 2 13 8 3 15 7 11 4 16 9 1 14 6 12

5 17 10 2 13 8 3 15 7 12 4 16 9 1 14 6 11

5 17 10 2 13 8 3 15 7 11 4 14 9 1 16 6 12

5 17 10 2 13 8 3 15 7 12 4 14 9 1 16 6 11

5 17 10 3 13 8 1 15 7 11 4 16 9 2 14 6 12

5 17 10 3 13 8 1 15 7 12 4 16 9 2 14 6 11

5 17 10 3 13 8 1 15 7 11 4 14 9 2 16 6 12

5 17 10 3 13 8 1 15 7 12 4 14 9 2 16 6 11

5 17 10 3 13 8 2 15 7 11 4 16 9 1 14 6 12

5 17 10 3 13 8 2 15 7 12 4 16 9 1 14 6 11

5 17 10 3 13 8 2 15 7 11 4 14 9 1 16 6 12

5 17 10 3 13 8 2 15 7 12 4 14 9 1 16 6 11

8 13 1 15 5 10 16 3 11 6 14 4 9 17 2 12 7

8 13 1 15 5 10 16 3 11 7 14 4 9 17 2 12 6

8 13 1 15 5 10 16 3 11 6 14 2 9 17 4 12 7

8 13 1 15 5 10 16 3 11 7 14 2 9 17 4 12 6

8 13 1 15 5 10 17 3 11 6 14 4 9 16 2 12 7

8 13 1 15 5 10 17 3 11 7 14 4 9 16 2 12 6

8 13 1 15 5 10 17 3 11 6 14 2 9 16 4 12 7

8 13 1 15 5 10 17 3 11 7 14 2 9 16 4 12 6

8 13 1 16 5 10 15 3 11 6 14 4 9 17 2 12 7

8 13 1 16 5 10 15 3 11 7 14 4 9 17 2 12 6

8 13 1 16 5 10 15 3 11 6 14 2 9 17 4 12 7

8 13 1 16 5 10 15 3 11 7 14 2 9 17 4 12 6

8 13 1 17 5 10 15 3 11 6 14 4 9 16 2 12 7

8 13 1 17 5 10 15 3 11 7 14 4 9 16 2 12 6

8 13 1 17 5 10 15 3 11 6 14 2 9 16 4 12 7

8 13 1 17 5 10 15 3 11 7 14 2 9 16 4 12 6

8 13 2 15 5 10 16 3 11 6 14 4 9 17 1 12 7

8 13 2 15 5 10 16 3 11 7 14 4 9 17 1 12 6

8 13 2 15 5 10 17 3 11 6 14 4 9 16 1 12 7

8 13 2 15 5 10 17 3 11 7 14 4 9 16 1 12 6

8 13 2 16 5 10 15 3 11 6 14 4 9 17 1 12 7

8 13 2 16 5 10 15 3 11 7 14 4 9 17 1 12 6

8 13 2 17 5 10 15 3 11 6 14 4 9 16 1 12 7

8 13 2 17 5 10 15 3 11 7 14 4 9 16 1 12 6

8 13 2 15 5 10 16 3 11 6 14 1 9 17 4 12 7

8 13 2 15 5 10 16 3 11 7 14 1 9 17 4 12 6

8 13 2 15 5 10 17 3 11 6 14 1 9 16 4 12 7

8 13 2 15 5 10 17 3 11 7 14 1 9 16 4 12 6

8 13 2 16 5 10 15 3 11 6 14 1 9 17 4 12 7

8 13 2 16 5 10 15 3 11 7 14 1 9 17 4 12 6

8 13 2 17 5 10 15 3 11 6 14 1 9 16 4 12 7

8 13 2 17 5 10 15 3 11 7 14 1 9 16 4 12 6

8 13 3 15 5 10 16 1 11 6 14 4 9 17 2 12 7

8 13 3 15 5 10 16 1 11 7 14 4 9 17 2 12 6

8 13 3 15 5 10 16 2 11 6 14 4 9 17 1 12 7

8 13 3 15 5 10 16 2 11 7 14 4 9 17 1 12 6

8 13 3 15 5 10 17 1 11 6 14 4 9 16 2 12 7

8 13 3 15 5 10 17 1 11 7 14 4 9 16 2 12 6

8 13 3 15 5 10 17 2 11 6 14 4 9 16 1 12 7

8 13 3 15 5 10 17 2 11 7 14 4 9 16 1 12 6

8 13 3 16 5 10 15 1 11 6 14 4 9 17 2 12 7

8 13 3 16 5 10 15 1 11 7 14 4 9 17 2 12 6

8 13 3 16 5 10 15 2 11 6 14 4 9 17 1 12 7

8 13 3 16 5 10 15 2 11 7 14 4 9 17 1 12 6

8 13 3 17 5 10 15 1 11 6 14 4 9 16 2 12 7

8 13 3 17 5 10 15 1 11 7 14 4 9 16 2 12 6

8 13 3 17 5 10 15 2 11 6 14 4 9 16 1 12 7

8 13 3 17 5 10 15 2 11 7 14 4 9 16 1 12 6

8 15 1 13 5 10 16 3 11 6 14 4 9 17 2 12 7

8 15 1 13 5 10 16 3 11 7 14 4 9 17 2 12 6

8 15 1 13 5 10 16 3 11 6 14 2 9 17 4 12 7

8 15 1 13 5 10 16 3 11 7 14 2 9 17 4 12 6

8 15 1 13 5 10 17 3 11 6 14 4 9 16 2 12 7

8 15 1 13 5 10 17 3 11 7 14 4 9 16 2 12 6

8 15 1 13 5 10 17 3 11 6 14 2 9 16 4 12 7

8 15 1 13 5 10 17 3 11 7 14 2 9 16 4 12 6

8 15 2 13 5 10 16 3 11 6 14 4 9 17 1 12 7

8 15 2 13 5 10 16 3 11 7 14 4 9 17 1 12 6

8 15 2 13 5 10 17 3 11 6 14 4 9 16 1 12 7

8 15 2 13 5 10 17 3 11 7 14 4 9 16 1 12 6

8 15 2 13 5 10 16 3 11 6 14 1 9 17 4 12 7

8 15 2 13 5 10 16 3 11 7 14 1 9 17 4 12 6

8 15 2 13 5 10 17 3 11 6 14 1 9 16 4 12 7

8 15 2 13 5 10 17 3 11 7 14 1 9 16 4 12 6

8 15 3 13 5 10 16 1 11 6 14 4 9 17 2 12 7

8 15 3 13 5 10 16 1 11 7 14 4 9 17 2 12 6

8 15 3 13 5 10 16 2 11 6 14 4 9 17 1 12 7

8 15 3 13 5 10 16 2 11 7 14 4 9 17 1 12 6

8 15 3 13 5 10 17 1 11 6 14 4 9 16 2 12 7

8 15 3 13 5 10 17 1 11 7 14 4 9 16 2 12 6

8 15 3 13 5 10 17 2 11 6 14 4 9 16 1 12 7

8 15 3 13 5 10 17 2 11 7 14 4 9 16 1 12 6

8 16 1 13 5 10 15 3 11 6 14 4 9 17 2 12 7

8 16 1 13 5 10 15 3 11 7 14 4 9 17 2 12 6

8 16 1 13 5 10 15 3 11 6 14 2 9 17 4 12 7

8 16 1 13 5 10 15 3 11 7 14 2 9 17 4 12 6

8 16 2 13 5 10 15 3 11 6 14 4 9 17 1 12 7

8 16 2 13 5 10 15 3 11 7 14 4 9 17 1 12 6

8 16 2 13 5 10 15 3 11 6 14 1 9 17 4 12 7

8 16 2 13 5 10 15 3 11 7 14 1 9 17 4 12 6

8 16 3 13 5 10 15 1 11 6 14 4 9 17 2 12 7

8 16 3 13 5 10 15 1 11 7 14 4 9 17 2 12 6

8 16 3 13 5 10 15 2 11 6 14 4 9 17 1 12 7

8 16 3 13 5 10 15 2 11 7 14 4 9 17 1 12 6

8 17 1 13 5 10 15 3 11 6 14 4 9 16 2 12 7

8 17 1 13 5 10 15 3 11 7 14 4 9 16 2 12 6

8 17 1 13 5 10 15 3 11 6 14 2 9 16 4 12 7

8 17 1 13 5 10 15 3 11 7 14 2 9 16 4 12 6

8 17 2 13 5 10 15 3 11 6 14 4 9 16 1 12 7

8 17 2 13 5 10 15 3 11 7 14 4 9 16 1 12 6

8 17 2 13 5 10 15 3 11 6 14 1 9 16 4 12 7

8 17 2 13 5 10 15 3 11 7 14 1 9 16 4 12 6

8 17 3 13 5 10 15 1 11 6 14 4 9 16 2 12 7

8 17 3 13 5 10 15 1 11 7 14 4 9 16 2 12 6

8 17 3 13 5 10 15 2 11 6 14 4 9 16 1 12 7

8 17 3 13 5 10 15 2 11 7 14 4 9 16 1 12 6

8 13 1 15 5 10 3 16 7 11 4 14 9 2 17 6 12

8 13 1 15 5 10 3 16 7 12 4 14 9 2 17 6 11

8 13 1 15 5 10 3 17 7 11 4 14 9 2 16 6 12

8 13 1 15 5 10 3 17 7 12 4 14 9 2 16 6 11

8 13 1 16 5 10 3 15 7 11 4 17 9 2 14 6 12

8 13 1 16 5 10 3 15 7 12 4 17 9 2 14 6 11

8 13 1 16 5 10 3 15 7 11 4 14 9 2 17 6 12

8 13 1 16 5 10 3 15 7 12 4 14 9 2 17 6 11

8 13 1 17 5 10 3 15 7 11 4 16 9 2 14 6 12

8 13 1 17 5 10 3 15 7 12 4 16 9 2 14 6 11

8 13 1 17 5 10 3 15 7 11 4 14 9 2 16 6 12

8 13 1 17 5 10 3 15 7 12 4 14 9 2 16 6 11

8 13 2 15 5 10 3 16 7 11 4 14 9 1 17 6 12

8 13 2 15 5 10 3 16 7 12 4 14 9 1 17 6 11

8 13 2 15 5 10 3 17 7 11 4 14 9 1 16 6 12

8 13 2 15 5 10 3 17 7 12 4 14 9 1 16 6 11

8 13 2 16 5 10 3 15 7 11 4 17 9 1 14 6 12

8 13 2 16 5 10 3 15 7 12 4 17 9 1 14 6 11

8 13 2 16 5 10 3 15 7 11 4 14 9 1 17 6 12

8 13 2 16 5 10 3 15 7 12 4 14 9 1 17 6 11

8 13 2 17 5 10 3 15 7 11 4 16 9 1 14 6 12

8 13 2 17 5 10 3 15 7 12 4 16 9 1 14 6 11

8 13 2 17 5 10 3 15 7 11 4 14 9 1 16 6 12

8 13 2 17 5 10 3 15 7 12 4 14 9 1 16 6 11

8 13 3 15 5 10 1 16 7 11 4 14 9 2 17 6 12

8 13 3 15 5 10 1 16 7 12 4 14 9 2 17 6 11

8 13 3 15 5 10 1 17 7 11 4 14 9 2 16 6 12

8 13 3 15 5 10 1 17 7 12 4 14 9 2 16 6 11

8 13 3 15 5 10 2 16 7 11 4 14 9 1 17 6 12

8 13 3 15 5 10 2 16 7 12 4 14 9 1 17 6 11

8 13 3 15 5 10 2 17 7 11 4 14 9 1 16 6 12

8 13 3 15 5 10 2 17 7 12 4 14 9 1 16 6 11

8 13 3 16 5 10 1 15 7 11 4 17 9 2 14 6 12

8 13 3 16 5 10 1 15 7 12 4 17 9 2 14 6 11

8 13 3 16 5 10 2 15 7 11 4 17 9 1 14 6 12

8 13 3 16 5 10 2 15 7 12 4 17 9 1 14 6 11

8 13 3 16 5 10 1 15 7 11 4 14 9 2 17 6 12

8 13 3 16 5 10 1 15 7 12 4 14 9 2 17 6 11

8 13 3 16 5 10 2 15 7 11 4 14 9 1 17 6 12

8 13 3 16 5 10 2 15 7 12 4 14 9 1 17 6 11

8 13 3 17 5 10 1 15 7 11 4 16 9 2 14 6 12

8 13 3 17 5 10 1 15 7 12 4 16 9 2 14 6 11

8 13 3 17 5 10 1 15 7 11 4 14 9 2 16 6 12

8 13 3 17 5 10 1 15 7 12 4 14 9 2 16 6 11

8 13 3 17 5 10 2 15 7 11 4 16 9 1 14 6 12

8 13 3 17 5 10 2 15 7 12 4 16 9 1 14 6 11

8 13 3 17 5 10 2 15 7 11 4 14 9 1 16 6 12

8 13 3 17 5 10 2 15 7 12 4 14 9 1 16 6 11

8 15 1 13 5 10 3 16 7 11 4 14 9 2 17 6 12

8 15 1 13 5 10 3 16 7 12 4 14 9 2 17 6 11

8 15 1 13 5 10 3 17 7 11 4 14 9 2 16 6 12

8 15 1 13 5 10 3 17 7 12 4 14 9 2 16 6 11

8 15 2 13 5 10 3 16 7 11 4 14 9 1 17 6 12

8 15 2 13 5 10 3 16 7 12 4 14 9 1 17 6 11

8 15 2 13 5 10 3 17 7 11 4 14 9 1 16 6 12

8 15 2 13 5 10 3 17 7 12 4 14 9 1 16 6 11

8 15 3 13 5 10 1 16 7 11 4 14 9 2 17 6 12

8 15 3 13 5 10 1 16 7 12 4 14 9 2 17 6 11

8 15 3 13 5 10 1 17 7 11 4 14 9 2 16 6 12

8 15 3 13 5 10 1 17 7 12 4 14 9 2 16 6 11

8 15 3 13 5 10 2 16 7 11 4 14 9 1 17 6 12

8 15 3 13 5 10 2 16 7 12 4 14 9 1 17 6 11

8 15 3 13 5 10 2 17 7 11 4 14 9 1 16 6 12

8 15 3 13 5 10 2 17 7 12 4 14 9 1 16 6 11

8 16 1 13 5 10 3 15 7 11 4 17 9 2 14 6 12

8 16 1 13 5 10 3 15 7 12 4 17 9 2 14 6 11

8 16 2 13 5 10 3 15 7 11 4 17 9 1 14 6 12

8 16 2 13 5 10 3 15 7 12 4 17 9 1 14 6 11

8 16 3 13 5 10 1 15 7 11 4 17 9 2 14 6 12

8 16 3 13 5 10 1 15 7 12 4 17 9 2 14 6 11

8 16 3 13 5 10 2 15 7 11 4 17 9 1 14 6 12

8 16 3 13 5 10 2 15 7 12 4 17 9 1 14 6 11

8 16 1 13 5 10 3 15 7 11 4 14 9 2 17 6 12

8 16 1 13 5 10 3 15 7 12 4 14 9 2 17 6 11

8 16 2 13 5 10 3 15 7 11 4 14 9 1 17 6 12

8 16 2 13 5 10 3 15 7 12 4 14 9 1 17 6 11

8 16 3 13 5 10 1 15 7 11 4 14 9 2 17 6 12

8 16 3 13 5 10 1 15 7 12 4 14 9 2 17 6 11

8 16 3 13 5 10 2 15 7 11 4 14 9 1 17 6 12

8 16 3 13 5 10 2 15 7 12 4 14 9 1 17 6 11

8 17 1 13 5 10 3 15 7 11 4 16 9 2 14 6 12

8 17 1 13 5 10 3 15 7 12 4 16 9 2 14 6 11

8 17 1 13 5 10 3 15 7 11 4 14 9 2 16 6 12

8 17 1 13 5 10 3 15 7 12 4 14 9 2 16 6 11

8 17 2 13 5 10 3 15 7 11 4 16 9 1 14 6 12

8 17 2 13 5 10 3 15 7 12 4 16 9 1 14 6 11

8 17 2 13 5 10 3 15 7 11 4 14 9 1 16 6 12

8 17 2 13 5 10 3 15 7 12 4 14 9 1 16 6 11

8 17 3 13 5 10 1 15 7 11 4 16 9 2 14 6 12

8 17 3 13 5 10 1 15 7 12 4 16 9 2 14 6 11

8 17 3 13 5 10 1 15 7 11 4 14 9 2 16 6 12

8 17 3 13 5 10 1 15 7 12 4 14 9 2 16 6 11

8 17 3 13 5 10 2 15 7 11 4 16 9 1 14 6 12

8 17 3 13 5 10 2 15 7 12 4 16 9 1 14 6 11

8 17 3 13 5 10 2 15 7 11 4 14 9 1 16 6 12

8 17 3 13 5 10 2 15 7 12 4 14 9 1 16 6 11

Pour N= 17 le nombre de solution est 768 ---------------

Le jeu des segments Ou irrégularités dans les distributions de séquence finie

IV Les solutions pour N0 = 17

Le jeu

des segments

Ou irrégularités dans les distributions de séquence finie