Chapitre I. La musique et les notes

Dans ce chapitre introductif, après quelques considérations générales sur le phénomène musical, on pose les premières pierres permettant d’aborder la question de la création et de la caractérisation des sons musicaux en termes physiques.

Chapitre I. La musique et les notes 1

I.1. Une première approche de la musique comme événement historique 2

I.2. Bruits et sons - TRANSITION ENTRE MUSIQUE ET PHYSIQUE 3

I.2.1. Généralités 3

I.2.2. Echelles et notes 3

I.2.3. Origine du nom des notes 7

I.2.4. Définition des gammes 7

I.2.5. Enchaînement des gammes 10

I.2.6. Définition d’un étalon 13

I.2.7. Transition vers la physique 14

I.3. Instruments de musique 15

I.3.1. Les grandes familles 15

I.3.2. Etendue des différents instruments 23

I.4. Annexe : Les différentes familles d’instruments de l’orchestre 24

I.5. Références 25

I.6. Liste des figures 26

I.1. Une première approche de la musique comme événement historique

Des différents « arts » qui font le génie humain, la musique comme le dessin trouve sans doute, si ce n’est son origine, du moins la raison de son évolution originelle dans la liturgie religieuse; depuis la préhistoire, elle devait accompagner les danses rituelles en en soulignant les rythmes. Pour marquer ce rythme, l’homme ne pouvait recourir qu’à des objets naturels capables de relayer sa propre voix, tels que des conques, coquillages, troncs d’arbres... les premières percussions. En même temps, il a pu appréhender, la voix étant libre, ses possibilités de vocalise et par la même, la notion de mélodie, synthèse de rythmes et de vocalises.

La technique progressant, l’homme a pu créer des objets musicaux de plus en plus sophistiqués, tels le lithophone - dont un exemplaire est conservé au musée de l’homme - ou bien les premiers instruments à cordes -tel l’arc dont le son produit par la corde tendue est consigné déjà dans l’Odyssée - ou à vents tels les flûtes ou les trompettes.

Dés le IV° millénaire avant J.C., en Mésopotamie, on voit apparaître un foisonnement d’instruments : harpes, sifflets, trompettes, cymbales, ..... On observe la même richesse en Egypte, mais ici, comme en Grèce plus tard, la musique franchit l’enceinte du temple pour gagner la rue et suivre une voie profane parallèle à son développement religieux. Ce seront les Grecs, avec leur amour de l’ordre universel qui commenceront à théoriser les premiers la musique, inventant les échelles, la première notation... Ce n’est néanmoins qu’à la fin du moyen âge que la théorie de la musique sera définie peu ou prou comme on la connaît aujourd’hui.

Des instruments utilisés et retrouvés dans les gisements archéologiques, on s’aperçoit que la musique a évolué du rythme pur vers la combinaison de sons « relativement purs » et de hauteurs différentes pour créer la mélodie : arcs à plusieurs cordes donnant les lyres et autres harpes, flûtes avec des tuyaux de longueurs différentes...

Rythme et son musical, sons de différentes hauteurs, mais sons « purs » tels qu’émis par des cordes tendues en vibrations, par des instruments à vents, voilà les premiers pas de la musique.

Dans cet ouvrage, nous allons vite abandonner la musique en tant qu’art ou qu’événement historique, pour se concentrer sur les raisons qui font qu’un instrument de musique produit des sons musicaux. On déterminera quels sont les principes physiques mis en jeu, et on en déduira quelques propriétés immédiates des instruments qui les mettent en œuvre. Nous nous focaliserons néanmoins sur les instruments à cordes, délaissant les instruments à vents ou à percussions.

I.2. Bruits et sons - TRANSITION ENTRE MUSIQUE ET PHYSIQUE

I.2.1. Généralités

Le son musical s’oppose au bruit de manière physiologique; le bruit étant perçu comme un agglomérat de sons. Une approche physique permet de faire une première distinction entre le bruit et le son musical. Les premiers instruments de musique à cordes ou à vent avaient comme particularité d’émettre des sons (voir le chapitre 4 pour une explication plus précise) pouvant être définis par une « hauteur », c’est à dire par une fréquence donnée. On peut donc essayer de définir le bruit par rapport au son musical, comme étant un agglomérat de fréquences composites; on définira un son « pur » comme étant un son de fréquence donnée, mesurable, constante. Un son musical sera soit un son pur, soit une combinaison de sons purs telle qu’un de ces sons purs soit prépondérant (on verra que l’on appelle ce son « le fondamental ») alors que les autres ont des intensités plus faibles (on les appellera « les harmoniques »). Ce sont ces harmoniques, ou plutôt la façon dont elles se composent, qui définissent le timbre d’un instrument. Grâce à un oscilloscope électronique nous visualiseront ces notions au chapitre 2.

Figure I‑1

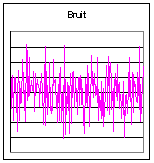
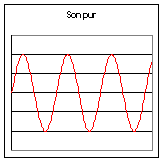
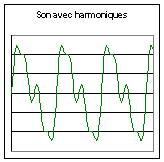
: Bruit et son

Ces notions ont été historiquement abordées depuis l’antiquité, et une compréhension « définitive » des phénomènes physiques mis en jeu n’a pu être acquise qu’a partir du XVIII° siècle.

I.2.2. Echelles et notes

L’oreille humaine est capable d’entendre des sons de fréquences pouvant aller de 15 à 20000 Hertz. Pour pouvoir « faire » de la musique, la reproduire, et surtout la communiquer, faire en sorte que plusieurs personnes puissent jouer la même musique, ensemble ou dans des lieux différents, il a fallu définir un ensemble représentatif des sons possibles pouvant servir de référence commune. Pour cela il a fallu faire une sélection dans l’ensemble des sons. Cette sélection s’accompagne forcément de la constitution d’une échelle.

La constitution de cette échelle a été évidemment variable d’une civilisation à l’autre, et a résulté de la confrontation des besoins musicaux aux possibilités offertes par les instruments de musique disponibles.

Pour définir une échelle, il a fallu définir une série de sons ascendants (du plus grave au plu aigu), chaque son étant défini de manière absolue, ou alors par rapport à celui qui le précède ou celui qui le suit. L’histoire, et la physique, ont montré que la méthode la plus facile était de définir une échelle de sons de manière relative (les uns par rapport aux autres). De plus l’utilisation des instruments à cordes ou à vent a très tôt du amener à l’observation que deux sons de fréquences différentes pouvaient « sonner » de manière très proche (voir chapitre 7); cette constatation a permis de définir la notion « d’octave », intervalle acoustique séparant deux notes « équivalentes ». Une fois l’octave définie, il est possible de définir un nombre quelconque de notes à l’intérieur de celle-ci et se répartissant dans l’intervalle acoustique ainsi déterminé. Historiquement, cet intervalle a été découpé en 12 notes.

Les premières observations « scientifiques » furent sans doute faites par Pythagore (è@ ) au VI° siècle avant J.C. [5]. A l’aide d’un instrument à corde (le monocorde), il remarqua, et sans doute pour résoudre des problèmes techniques d’accord des instruments, qu’une corde pincée en son milieu, produisait le même son que quand elle était libre, mais un son d’une octave supérieure (c’est à dire comme on le comprendra au chapitre 4, d’une fréquence double). Il constata aussi que cette corde, si on suppose qu’elle émet un Do actuel, pincée au 2/3 ou au ¾ produisait des sons différents; en fait respectivement notre Sol et notre Fa actuel. Cette succession est schématisée sur la suivante.

Figure I‑2 : Quinte

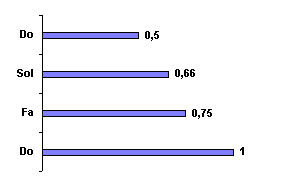
L’intervalle séparant le Do du Sol, ou plutôt le son produit par une corde de longueur L de celui produit par une corde de longueur 2/3 L, est appelé une « quinte » .

De nombreuses constructions sont réalisables à partir de cette constatation; par exemple on peut essayer de définir une gamme en enchaînant les quintes en partant du Do comme dans le graphique 1-83 ou N1(N2) signifie que N1 est obtenue comme quinte de N2; comme si on applique cette opération, on va vers l’aigu de plus d’une octave (c’est à dire que l’on obtient des longueurs inférieures à 0,5), on a re-normalisé chaque note changeant d’octave (en multipliant la longueur obtenue par 2ⁿ de façon à obtenir une longueur comprise entre 0,5 et 1).

Nous allons faire cette construction de manière graphique ; la figure ci dessous en montre le résultat pour une soixantaine d’occurrences. Plutôt que de tracer la longueur de la corde, on a préféré tracer une grandeur homogène à une fréquence sur la base de la propriété évoquée ci-dessus qui entraîne que les fréquences sont inversement proportionnelles à la longueur de la corde.

On constate sur un diagramme en fréquence, que cette fonction est « presque » périodique ; en effet, toutes les 12 occurrences on se retrouve à la fréquence « 1 », et les points modulo 12 sont pratiquement alignés verticalement, les écarts entre chacune étant à peu près égaux (on vérifiera plus loin que les écarts entre les logarithmes des fréquences sont effectivement pratiquement égaux. On constate également que sur les 12 intervalles ainsi constitués, les sept premières occurrences « partagent » le champs des fréquences de manière équilibrée (à part la septième néanmoins). Les figurent ci dessous illustre ces assertions.

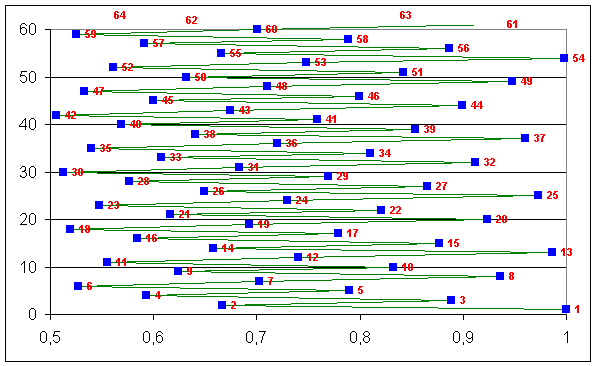
Figure I‑3 : répartition des fréquences après 60 « quintes »

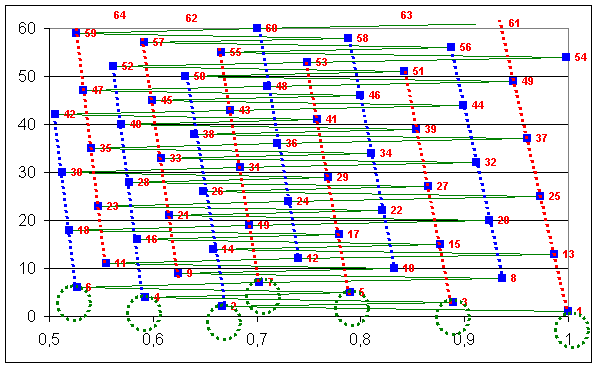
Figure I‑4 : Identification des notes et de la périodicité
Sur cette base, on peut définir une échelle de note soit de 12 notes, soit de six notes. Historiquement, les six notes ainsi définies constituent la gamme diatonique naturelle (voir figure ci-dessous ou on a représenté une octave).

Figure I‑5 : Une octave

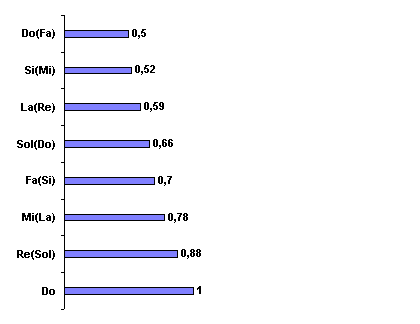
L’enchaînement des quintes est le suivant:

Do à Sol à Ré à La à Mi à Si à Fa à Do

Et l’ordre des fréquences est : do, ré, mi, fa, sol, la, si.

On vérifiera avec le tableau 3-1 que cette construction rend pratiquement compte des notes telles qu’on les connaît aujourd’hui.

Cette gamme est appelée « gamme diatonique naturelle ».

On remarquera que dans ce processus on a considéré que l’intervalle de quinte était indépendant de la note de départ, mais ne dépendait que du rapport des fréquences (en fait des longueurs, mais on verra au Chapitre 4 que la fréquence de la note est inversement proportionnelle à la longueur de la corde qui la produit). Cet intervalle de quinte correspond à un rapport de fréquence entre les deux notes de 3/2.

Cet accord de quinte est ainsi nommé, car la quinte d’une note se trouve être la cinquième note suivante dans l’ordre de la gamme. On définit de même les écarts de seconde, tierce, quarte, sixième, septième et d’octave.

On remarquera aussi sur la figure …. Que la 53° quinte redonne presque exactement la fréquence « 1 » ; ce qui a conduit certains à considérer chacune des 53 notes ainsi constituées comme des notes à part entière, séparées entre elles par une grandeur que l’on a nommé comma : donc 1/53 d’octave.

I.2.3. Origine du nom des notes

Le nom des notes a longtemps rendu compte de l’ordre dans lequel elles se succédaient, comme la notation actuelle anglophile ou germanophile : A,B,C,D,E,F,G et augmenté de H pour les germanophiles. Les noms des notes tels qu’on les connaît dans les pays de langue latine ont été choisies par Gui d’Arezzo au XI° siècle comme étant les premières syllabes des hémistiches des premiers vers de l’hymne des vêpres de l’office de Saint Jean Baptiste:

Figure I‑6 : Hymne de saint jean

" Pour que puissent résonner sur les cordes détendues de nos lêvres les merveilles de tes actions, enlève le péché de ton impur serviteur, ô Saint Jean." (Paul Diacre 730/799)

La correspondance entre les notes « latines » et « germano-anglophones » est la suivante :

A B C D E F G

La Si Do Ré Mi Fa Sol

et en langue allemande Si est désigné par H alors que B désigne Si^b

I.2.4. Définition des gammes

Un instrument (comme un piano par exemple) accordé en suivant la méthode explicitée ci-dessus sonnerait étrangement à nos oreilles modernes; certains intervalles entre les notes paraîtraient trop grands, d’autre trop petits. La méthode d’accord dite par tempérament égal opère sur les instruments à clavier une subdivision réductible à une unité simplifiée: le demi-ton [5].

L’explication de cet ajustement permet d’aborder quelques notions préliminaires liées aux différentes orientations que le phénomène musical est susceptible de suivre [5].

La musique peut d’abord évoluer dans la direction de la complexité mélodique: elle négligera alors la superposition des sons au profit de leur succession. Dans un désir de variété, elle tendra à la multiplication des échelles (musique de l’Inde), au fractionnement des intervalles (musique arabe). La gamme diatonique, avec ou sans intervalles inégaux, s’accommodera d’une telle préoccupation. Elle sera utilisable à cette fin aussi bien sous sa forme originelle que sous des formes dérivées. De nouvelles échelles seront ainsi bâties; soit naturellement en déplaçant les notes de départ et d’arrivée(ex.: de Ré à Ré, de Mi à Mi, etc., selon la technique médiévale); soit artificiellement par toute autre combinaison. Cette organisation de l’échelle est appelée le mode dont la formule sera celle de la distribution de ses intervalles. La musique procédant de cet esprit est dite modale [5].

A l’inverse, la musique peut orienter son développement vers l’émission simultanée des sons musicaux. Elle devra enchaîner non plus des sons simples, mais des groupes de sons de hauteurs distinctes. Elle s’intéressera alors aux affinités entre ces sons et à leur hiérarchisation. Elle cherchera sa diversité dans la richesse de leur étagement et assurera son unité en réduisant à l’essentiel la question de l’échelle. Celle-ci devra être simple et permettre la translation des hauteurs, tendant ainsi à l’uniformisation des intervalles. Sous réserves de quelques détails supplémentaires, le système construit sur ce principe est qualifié de tonal [5].

La musique européenne est passée progressivement de la première à la seconde des ces conceptions. Amorcé aux alentours du IX° siècle, ce mouvement a abouti aux environs des XVII° et XVIII° siècles à la survivance des deux échelles encore en service aujourd’hui [5].

Mode Majeur :

les tons se répartissent de la manière suivante:

1 1 1/2 1 1 1 ½ Cliquez ici pour écouter la gamme: gamme majeure

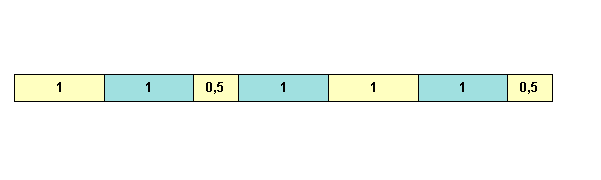
Figure I‑7 : Succession des tons : Mode majeur

Mode Mineur :

les tons se répartissent de la manière suivante:

1 1/2 1 1 1/2 1+1/2 ½ Cliquez ici pour écouter la gamme: gamme mineure

Figure I‑8 : Succession des tons : Mode Mineur

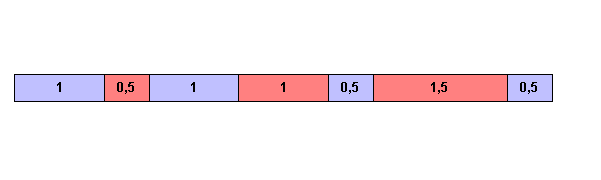
Ces modes sont adaptables à chaque degré de l’échelle des demi-tons. La gamme de Do majeur sera la gamme commençant à Do et avec les intervalles du mode majeur (touches blanches du piano). La gamme de La mineur, sera la gamme commençant à La et avec les intervalles du mode mineur.

Néanmoins, et on le verra par la suite lors de la définition des harmoniques et lors de l’approche de la théorie des accords, cette séparation en ½ tons n’est pas toujours respectée car non optimale. Pour certains instruments, il y a eu nécessité de définir des intervalles plus petits que l’on a nommé « commas »; il y a 9 commas dans un ton, et on a défini deux ½ tons différents, le demi ton chromatique valant 4 commas et le demi-ton diatonique valant 5 commas.

On peut alors construire les différentes gammes possibles, dans les modes mineurs et majeurs ; elles sont illustrées sur les figures 1-9 et 1-10.

Figure I‑9 : Succession des gammes : Mode Majeur

Mode majeur:

Do^#

Re^#

Fa^#

Sol

Sol^#

La^#

Do^#

Ré

Ré^#

Fa^#

Sol

Sol^#

La^#

Sol

Do^#

Re^#

Fa^#

Sol

La^#

Do^#

Fa^#

Sol

Do^#

Ré

Re^#

Sol

Sol^#

La^#

Ré

Ré^#

Fa^#

Sol^#

Do^#

Ré^#

Sol

La^#

Ré

Fa^#

Sol^#

La^#

Do^#

Ré^#

Fa^#

Sol

Ré

Fa^#

Sol

Sol^#

La^#

Do^#

Ré^#

Sol

Sol^#

Do^#

Ré

Fa^#

Sol^#

La^#

Ré

Ré^#

Sol

La^#

Do^#

Ré^#

Fa^#

Sol^#

La^#

On constate que pour quelques gammes, on ne retrouve pas le nom de chacune des 7 notes, mais deux fois la même note avec une altération en #; dans ce cas l’usage est d’utiliser la note supérieure avec son altération « bémol » de façon à bien retrouver chaque note de la gamme. Par exemple, la gamme de Ré^# s’appellera gamme de Mi^b. De même la gamme :

Fa, Sol, La, La^#, Do, Ré, Mi, Fa

se notera :

Fa, Sol, La, Si^b, Do, Ré, Mi, Fa.

(en faisant l’hypothèse d’un accord tempéré ou les dièses et les bémols correspondent exactement à des ½ ton).

Figure I‑10 : Succession des gammes : Mode Mineur

Mode mineur:

Do^#

Re^#

Fa^#

Sol

Sol^#

La^#

Do^#

Ré

Ré^#

Fa^#

Sol

Sol^#

La^#

Re^#

Sol

Sol^#

Do^#

Re^#

Fa^#

Sol^#

Do^#

Sol

La^#

Do^#

Ré

Re^#

Fa^#

Sol^#

La^#

Ré

Ré^#

Fa^#

Sol

Ré^#

Sol

Sol^#

La^#

Do^#

Fa^#

Sol^#

Do^#

Ré

Fa^#

Sol

La^#

Ré

Ré^#

Fa^#

Sol

Sol^#

La^#

Do^#

Ré^#

Sol

Sol^#

Ré

Sol^#

La^#

Do^#

Ré^#

Fa^#

La^#

Do^#

Ré

Fa^#

Sol

La^#

I.2.5. Enchaînement des gammes

Pour le mode majeur, on constate que pour chaque gamme de 8 notes, les quatre notes (tétracorde) supérieures présentent entre elles les même écarts que les quatre notes inférieures (1 - 1 - 0.5).

Ainsi, on peut choisir d’enchaîner les gammes, en transformant soit le tétracorde supérieur d’une gamme en tétracorde inférieur de la suivante (ordre des « dièses »), soit en transformant le tétracorde inférieur d’une gamme, en tétracorde supérieur de la suivante (ordre des « bémols »).

Par exemple, dans le premier cas, si on part de la gamme de Do majeur, la gamme suivante commence à Sol et comporte un seul dièse : Fa^#; la suivante est la gamme de Ré et comporte deux dièses Fa^# et Do^#; et si on continue de cette façon, on retombe au bout de 7 séquences sur la gamme de Do. Les gammes obtenues ont dans l’ordre 1 puis 2 puis 3 puis.... puis 7 dièses qui sont dans l’ordre:

Fa, Do, Sol, Ré, La, Mi, SI.

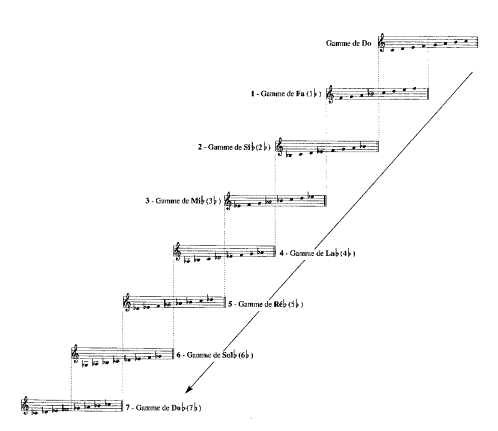
Si maintenant on pratique la seconde méthode en partant de la gamme de Do, la gamme suivante est celle qui se termine par Do, Ré, Mi, Fa; La seule possible est alors la gamme de Fa, ou le La^# est nommé Si^b suivant la remarque de la page précédente. Si on continue de la sorte, on retrouve la même construction que précédemment, mais cette fois en introduisant des « bémols » au lieu des « dièses ». La succession des bémols se fait dans l’ordre:

Si, Mi, La, Ré, Sol, Do, Fa.

Sur les deux figures suivantes (1-11 et 1-12 ) on a représenté la succession des gammes dans les deux méthodes [4].

Figure I‑11 : ENCHAINEMENT DES GAMMES (Ordre des dièses)

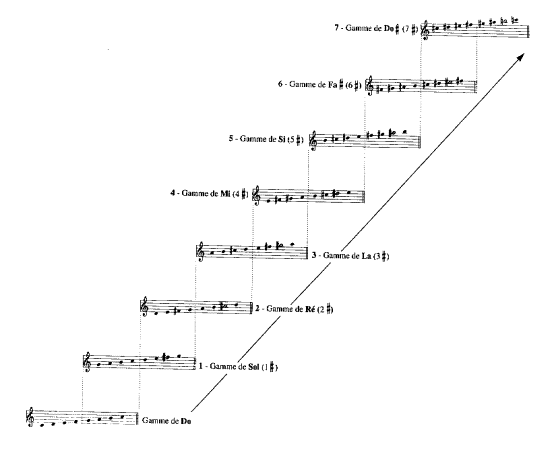
Figure I‑12 : ENCHAINEMENT DES GAMMES (Ordre des bémols)

I.2.6. Définition d’un étalon

La définition des gammes telles que décrite au §2.3, a permis de disposer d’un référentiel relatif commun. Le problème technique qui restait à résoudre était de définir un repère absolu, c’est à dire de définir des moyens permettant d’être sur qu’une note donnée correspondait vraiment au même son quels que soient l’interprète ou le moment. Pour cela, il suffisait de pouvoir définir, pour au moins une note donnée, une fréquence de référence. Après un long flottement, et grâce à l’invention en 1711 par l’Anglais John Shore du diapason, instrument capable d’émettre un son sans harmoniques, la note de référence a été fixée à 440 Hertz pour le LA₃.

Le diapason est un petit instrument qui produit un son invariable de référence. Il peut être de formes diverses mais le plus répandu est le « diapason à fourche » constitué d’une tige en acier recourbée en U. La hauteur absolue de ce La du diapason a été normalisée en 1859 seulement en France à 435 Hertz (soit 870 vibrations simples à la seconde); l’étalon en est déposé au Conservatoire National Supérieur de Musique de Paris. En 1953, par la convention internationale de Londres, toujours en vigueur, la hauteur absolue a été, en théorie, normalisée à 440 Hertz. Néanmoins, en pratique, on constate que cette convention n’est pas scrupuleusement suivie et l’on observe vers la fin du Xxe siècle une dérive variable, selon les pays et les genres de musique, autour de 440-445 Hertz.

Figure I‑13 : Un diapason

I.2.7. Transition vers la physique

Du phénomène historico-culturel qu’est la musique en tant qu’art majeur, on a tenté dans les paragraphes précédents de définir de manière physique, et en se fondant sur la technique qui a conduit à l’état actuel de la théorie de la musique, l’élément de base de cet art qu’est la note. Pour le moment, nous avons seulement défini la note comme étant un son caractérisable par une fréquence donnée. L’expérience montre néanmoins qu’une note donnée, jouée par un piano, une flûte ou un orgue n’est pas perçue par l’oreille de la même façon bien qu’il soit possible de distinguer que c’est bien à la base la même. Ce qui différencie ces différentes « notes » c’est le « timbre ». Le timbre est une caractéristique de l’instrument. Pour comprendre ce qu’est le timbre, et au delà, pour comprendre ce qu’est une note de musique telle qu’effectivement jouée par un instrument, il est nécessaire de comprendre d’abord comment est créée une note; d’en comprendre les mécanismes physiques qui conduisent à la perception du son par l’oreille, et de comprendre comment ces mécanismes définissent en fait le timbre des instruments.

Après avoir passé en revue rapidement les grandes familles d’instruments de musique dans le paragraphe suivant, les chapitres suivants vont progressivement essayer d’aborder ces questions sur l’exemple des instruments à cordes. Pour cela, après un chapitre 2 consacré à une étude expérimentale de différents sons pour mieux apprécier et visualiser leurs caractéristiques ;on tentera dans le chapitre 3 d’établir une définition « absolue » des différentes gammes, le chapitre 4 traitera de la génération d’une vibration sur une corde tendue. Les chapitres 5 et 6 examineront comment cette vibration peut être transférée à l’air et donc produire un son. Le chapitre 7 quant à lui montrera comment, à partir des résultats du chapitre 3, on peut expliquer ce qui sous-tend la notion d’harmonie en traitant de la justification des accords. Enfin les chapitre 8, 9 et 10 traiteront plus spécifiquement des instruments à cordes pincées, frappées et frottées et donneront quelques éléments de conception de ces instruments.

I.3. Instruments de musique

I.3.1. Les grandes familles

Un instrument de musique est un objet qui, lorsque qu’excité, peut émettre un ou plusieurs sons musicaux, et idéalement, émettre des sons calés sur la gamme utilisée.

Depuis l’antiquité, de nombreuses possibilités pour obtenir ce résultat ont été testées et développées, de la plus simple à la plus sophistiquée. On distingue plusieurs « classes » d’instruments de musique en fonction des moyens utilisés pour créer le son. On distingue trois classes principales qui sont les instruments à vents, les instruments à corde et les percussions.

Les instruments à vent, tels les flûtes, hautbois, trompettes, cors, mais aussi orgues, harmonium, ...ou c’est le souffle de l’interprète (ou bien un courant d’air fourni par un soufflet, une pompe, ...) qui permet la création du son.

Figure I‑14 : Exemples d’instruments à vents

Helicon

Basson

Galoubet

Fifre

Cor Anglais

Hautbois

Clarinette

Clairon

Serpent


Saxophone alto	Saxophone baryton	Saxophone soprano

Saxophone ténor

Bugle

Cornet à pistons

Cor de chasse

Cor à pistons

Trompette

Trombone à coulisse

Trombone à pistons

Flute de Pan

Sarrussophone

Harmonicor

Cornemuse

Musette

Ocarina

Harmonica

Accordéon

Mirliton

Serinette

Harmonium

Orgues

Dans cette classe d’instruments on distingue encore des familles qui sont définies par des similarités de timbre. Les principales familles sont les bois et les cuivre (voir annexe).

Les instruments à corde, tels que les violons, contrebasses, clavecins, pianos, guitares, harpes,... pour lesquels le son est créé par une corde mise en vibration par divers procédés. En fonction du procédé utilisé, on distingue différentes familles: les cordes pincées (guitare, clavecin), les cordes frappées (piano) et les cordes frottées (violon,...) - Voir annexe -.

Figure I‑15 : Exemples d’instruments à cordes

Guitare

Luth

Banjo

Vielle

Cithare

Lyre

Harpe

Clavecin

Epinette


Piano droit	Piano à queue	Violon alto

Violon

Violoncelle

Contrebasse

Viole d’amour

Mandoline

Monocorde

Clavicorde

Les instruments à percussions tels que les tambours, cymbales, triangle, xylophone, ... pour lesquels le son est émis après percussion d’une membrane, d’une lame, d’un tuyau, ....

Dans cette classe on distingue la familles des instruments à intonation définie de celle des instruments à intonation indéfinie (Voir annexe).

Figure I‑16 : Exemples d’instruments à percussions

Carillon

Castagnettes

Cloche

Guimbarde

Timbale

Triangle


Cymbales	Grelots	Grosse caisse

Xylophone

Marimbas

Congas

Tambourin

Tambourin …

Tambourin ….

Enfin, les progrès récents de l’analyse des signaux, mais surtout de l’électronique, quelle soit numérique ou analogique, ont permis d’abord d’analyser les sons émis par les différents instruments, et ensuite de les synthétiser à l’aide de procédés électroniques. Parfois même, en plus du son, on est arrivé à simuler l’instrument lui-même comme dans le cas des pianos, ou, dans une certaine mesure, le touché est rendu et simulé.

On a vu par ce rapide survol, qui est loin d’être exhaustif, l’extraordinaire inventivité dans la réalisation des instruments de musique, preuve, si besoin est, de la haute place que tient la musique dans la civilisation.

I.3.2. Etendue des différents instruments

Les différents instruments passés en revue ci-dessus permettent de couvrir une large gamme de fréquences; leur utilisation simultanée permet de disposer de toutes les hauteurs de son. Sur le tableau ci-après, on a indiqué pour les principaux instruments de l’orchestre (voir annexe) leur registre en notes (voir les valeurs des fréquences dans le chapitre 3), et on a ajouté le registre de la voix humaine.

Figure I‑17 : Etendue des instruments

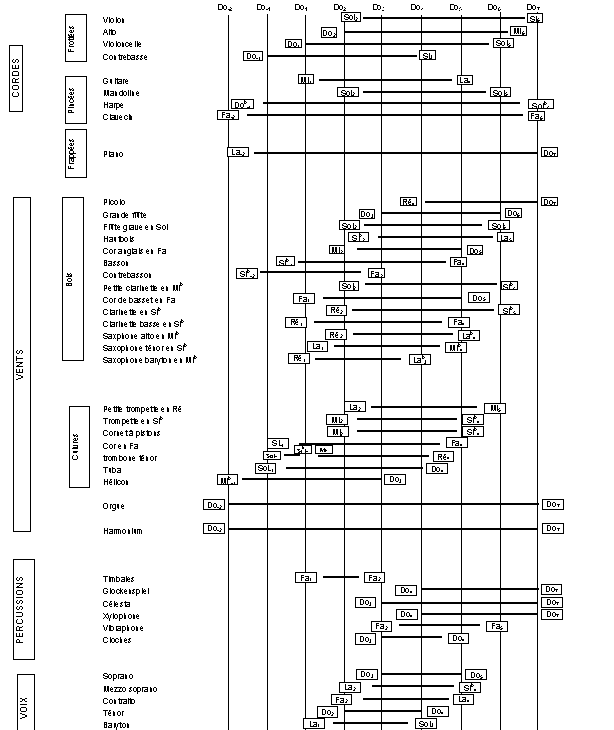
I.4. Annexe : Les différentes familles d’instruments de l’orchestre

Instruments à vent	Bois	La flûte et le piccolo Le hautbois et le cor anglais Le basson - le contre-basson La clarinette Le saxophone
	Cuivre	La trompette - Le cor - Le trombone Le tuba
Instruments à percussion	à intonation définie	Les timbales Le xylophone Le vibraphone Le glockenspiel Le céleste les cloches
	à intonation indéfinie	Les triangles Les cymbales Le gong Le tam-tam Les tambours
Instruments à cordes	à cordes pincées	L’épinette Le clavecin La harpe Le luth La mandoline la guitare
	à cordes frappées	Le monocorde Le clavicorde Le piano
	à cordes frottées	Le violon La contrebasse la vielle